数据结构-算法复杂度

First Post:

Last Update:

Page View: loading...

算法复杂度

算法复杂度旨在计算在输入数据量 N的情况下，算法的「时间使用」和「空间使用」情况；体现算法运行使用的时间和空间随「数据大小 N」而增大的速度。

算法复杂度主要可从 时间 、空间 两个角度评价：

  • 时间： 假设各操作的运行时间为固定常数，统计算法运行的「计算操作的数量」 ，以代表算法运行所需时间；
  • 空间： 统计在最差情况下，算法运行所需使用的「最大空间」；

「输入数据大小N」指算法处理的输入数据量；根据不同算法，具有不同定义，例如：

  • 排序算法： N代表需要排序的元素数量；
  • 搜索算法： N代表搜索范围的元素总数，例如数组大小、矩阵大小、二叉树节点数、图节点和边数等；

接下来，我们将分别从概念定义、符号表示、常见种类、时空权衡、示例解析、示例题目等角度入手，学习「时间复杂度」和「空间复杂度」。

时间复杂度

代码执行次数的简化估算值就是时间复杂度。

一些例子

  1. 线性复杂度O(N)：单层循环，如遍历数组求和。

  2. 对数复杂度O(logN)：二分查找。

  3. 线性对数复杂度O(NlogN)：快速排序或归并排序的分治策略。

  4. 平方复杂度O(N^2)：双重循环，如冒泡排序。

  5. 指数复杂度O(2^N)：递归斐波那契。

  6. 阶乘复杂度O(N!)：全排列生成。

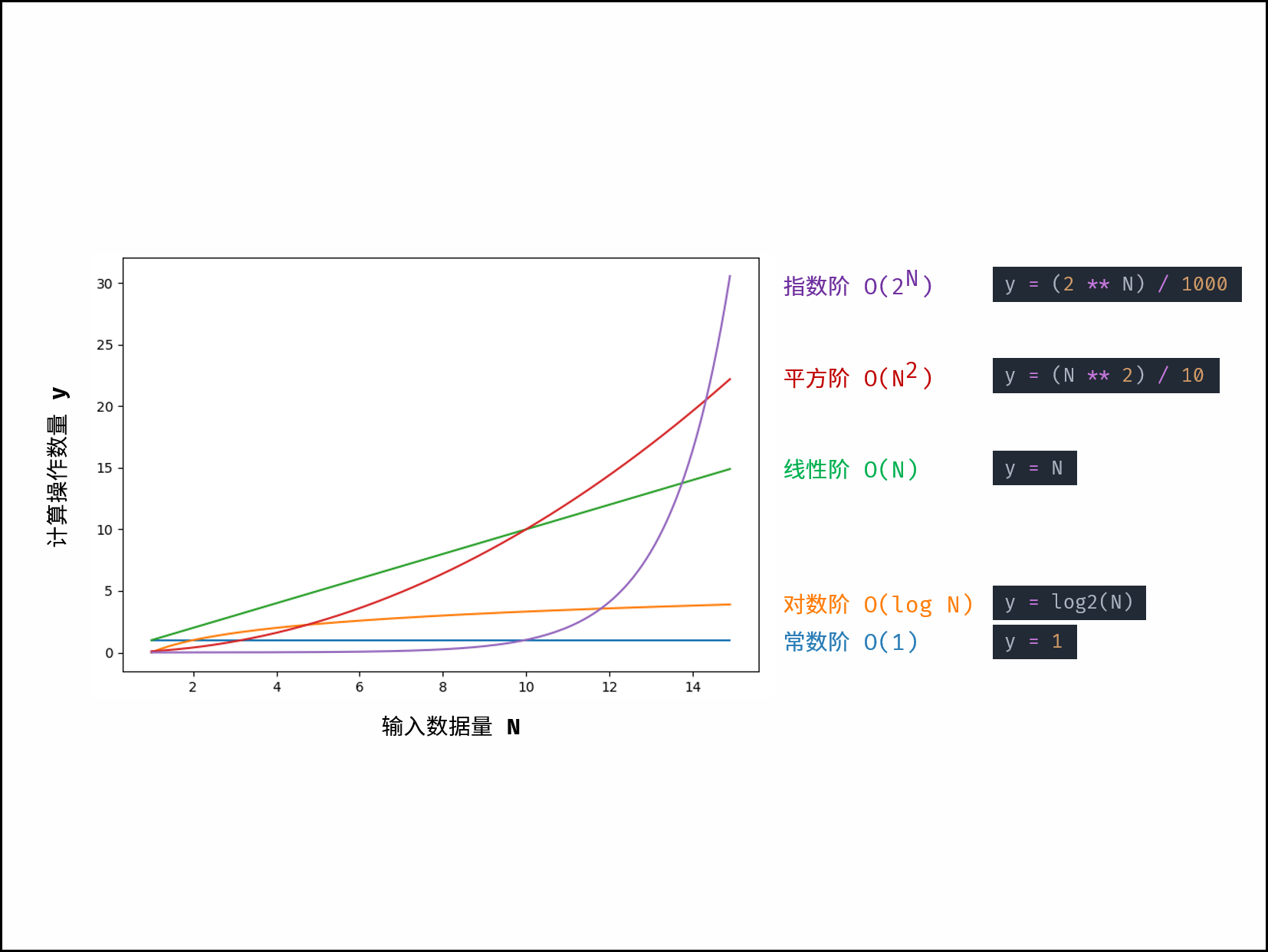
其中有：O(1)<O(logN)<O(N)<O(NlogN)<O(N^2)<O(2^N)<O(N!)

基本复杂度计算

层层（循环、递归）相加：比如有2层循环，第一层循环共执行n次基本语句，每个基本语句执行1次，也就是n个“1”次相加，为n；第二层循环执行log2n次第一次循环，每个第一次循环执行n次，总的也就是log2n个“n”次相加为nlog2n，故时间复杂度为O(nlogn)。

复杂度计算的核心规则

  1. 单层循环：直接取循环次数，如 O(n).
  2. 嵌套循环：各层循环次数相乘，如 O(n²) 或 O(n log n).
  3. 递归算法：
    • 递归次数 × 每次递归的操作次数，如斐波那契数列的 O(2ⁿ).
    • 分治策略（如归并排序）通过主定理计算，结果为 O(n log n).
  4. 忽略低阶项：如 T(n) = 3n² + 2n + 1 简化为 O(n²).

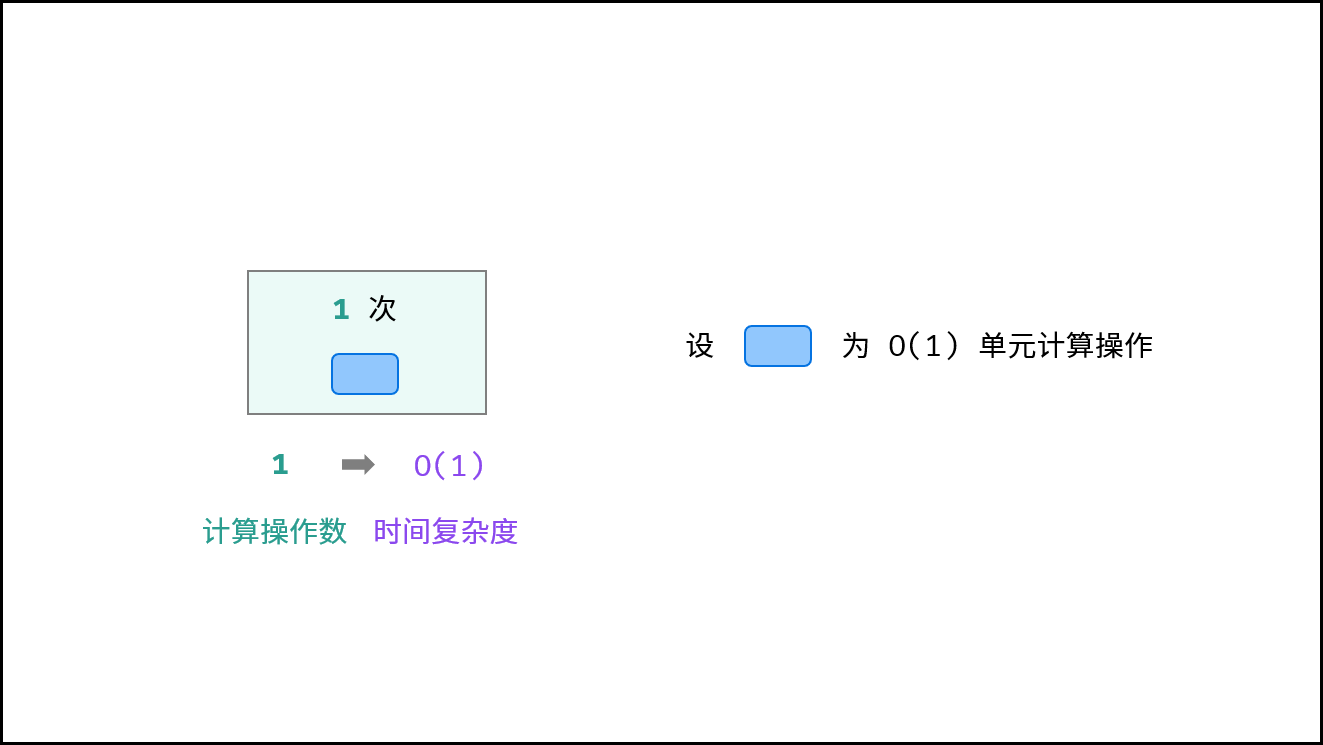
1. O(1) — 常数复杂度

特点：运行次数与 N 大小呈常数关系，即不随输入数据大小 N 的变化而变化。

示例：访问数组元素或交换变量。 

1
2
3
4
5
6
7
8
9
10
11
// 访问数组元素
int getElement(int arr[], int index) {
    return arr[index]; // 无论数组大小，直接访问固定位置
}

// 交换变量
void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp; // 仅需三次赋值操作
}

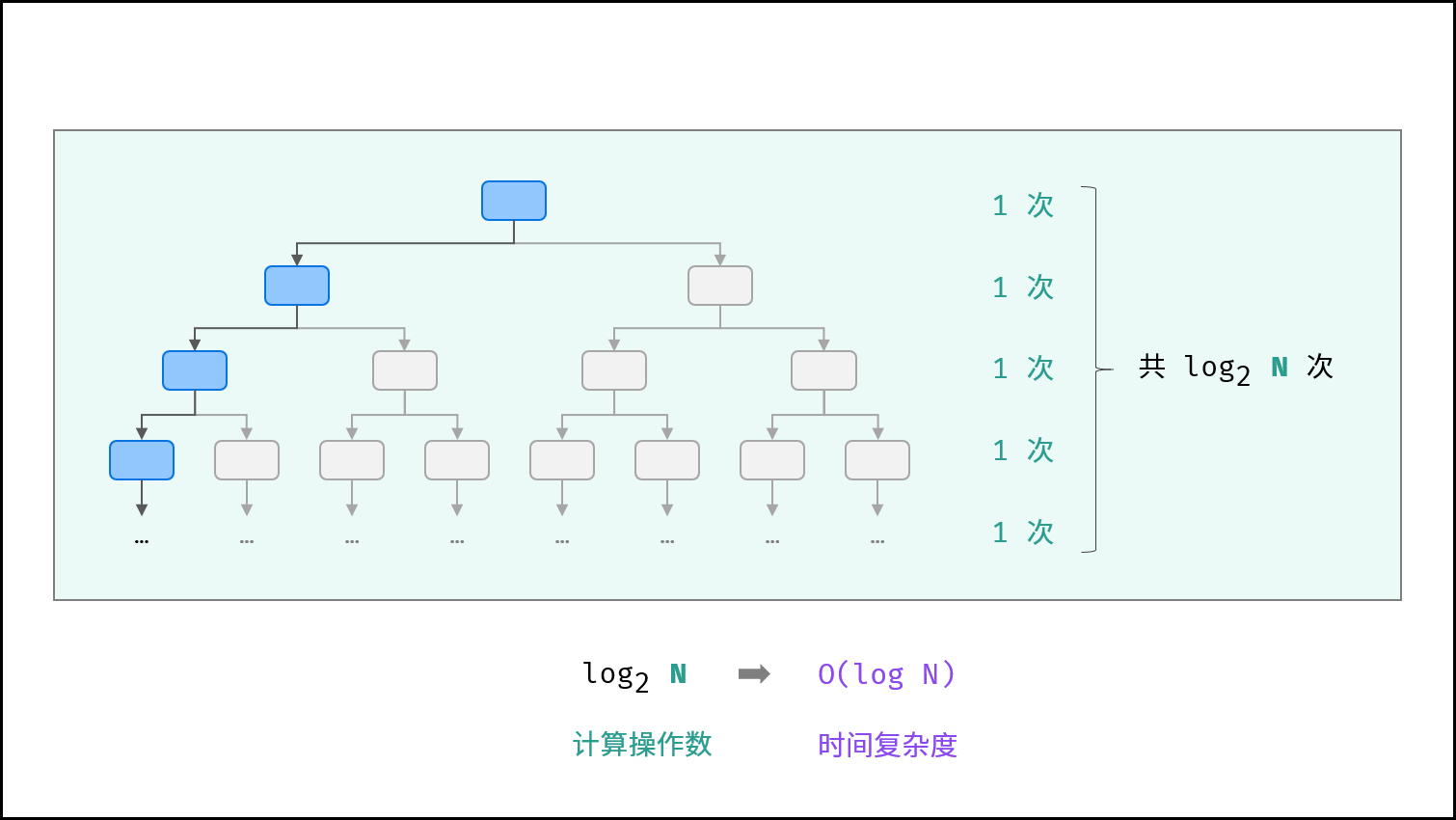
2. O(log n) — 对数复杂度

特点：每次操作将问题规模缩减为固定比例（如折半）。
示例：二分查找。 

1
2
3
4
5
6
7
8
9
int binarySearch(int arr[], int left, int right, int target) {
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == target) return mid;
        if (arr[mid] < target) left = mid + 1;
        else right = mid - 1; // 每次搜索范围减半
    }
    return -1;
}

如下图所示，为二分查找的时间复杂度示意图，每次二分将搜索区间缩小一半。

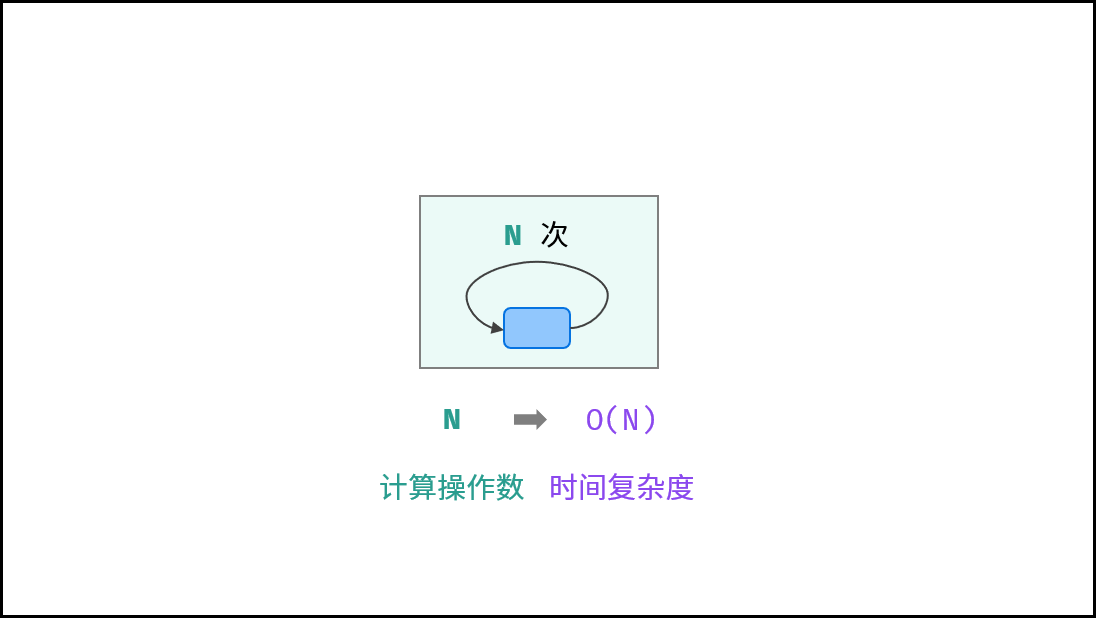
3. O(n) — 线性复杂度

特点：执行时间与输入规模成线性正比。
示例：遍历数组求和。 

1
2
3
4
5
6
7
int sumArray(int arr[], int size) {
    int sum = 0;
    for (int i = 0; i < size; i++) {
        sum += arr[i]; // 遍历所有元素，执行次数为n
    }
    return sum;
}

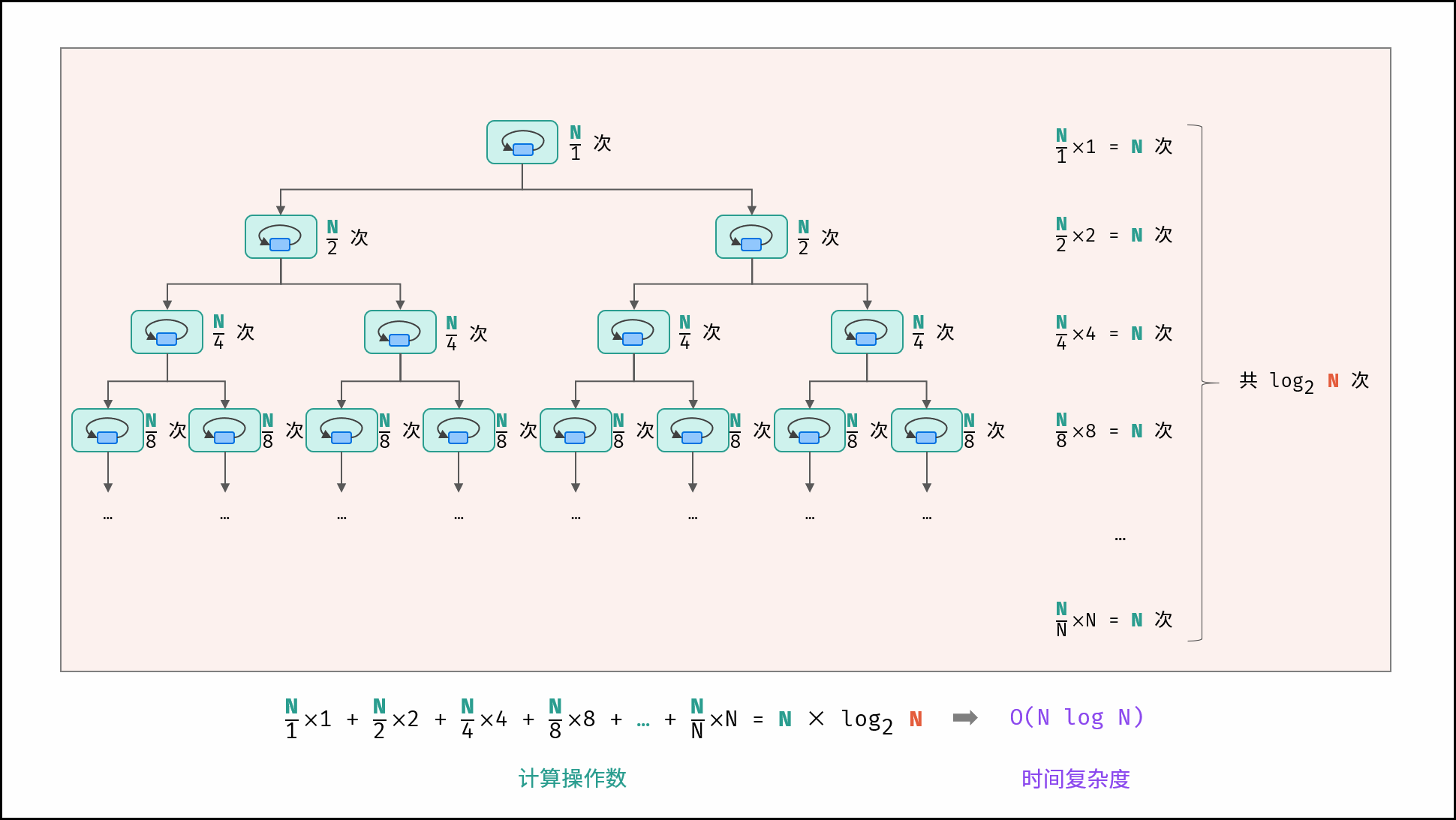
4. O(n log n) — 对数线性复杂度

特点：两层循环相互独立，第一层和第二层时间复杂度分别为 O(log⁡N) 和 O(N)，则总体时间复杂度为 O(Nlog⁡N)

结合线性与对数操作，常见于分治算法。
示例：快速排序。 

1
2
3
4
5
6
7
8
void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pivot = partition(arr, low, high); // 分区操作O(n)
        quickSort(arr, low, pivot - 1);  // 递归左半部分
        quickSort(arr, pivot + 1, high); // 递归右半部分
    }
}
// 每次递归将问题规模分半，递归深度为log n，每层总操作次数为n

线性对数阶常出现于排序算法，例如「快速排序」、「归并排序」、「堆排序」等，其时间复杂度原理如下图所示。

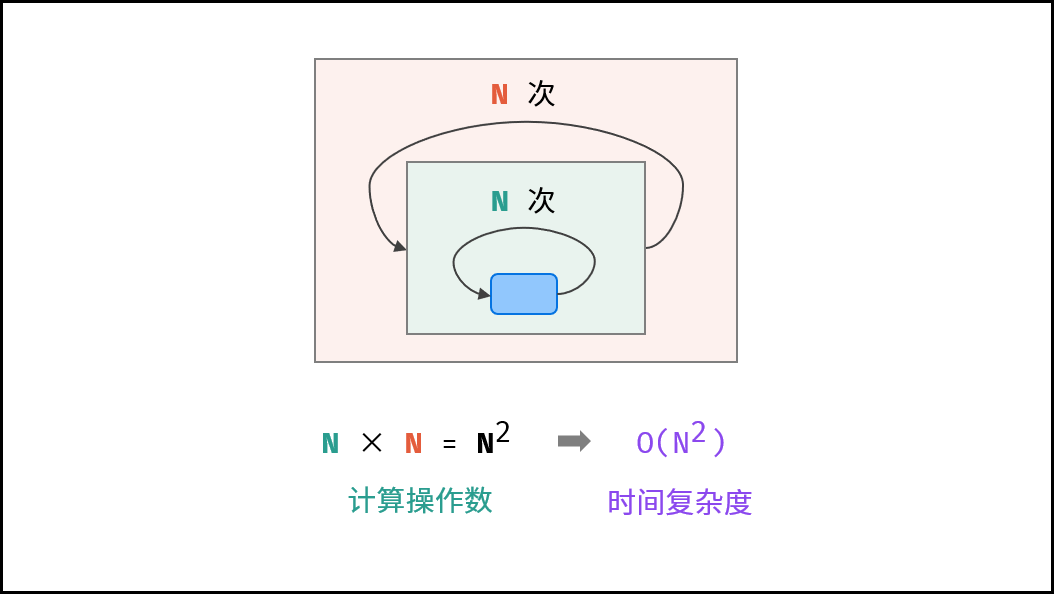
5. O(nᵏ) — 多项式复杂度（k=2为例）

特点：嵌套循环导致时间复杂度为输入规模的k次方。
示例：冒泡排序。 第一层和第二层时间复杂度分别为 O(N) 和 O(N)，则总体时间复杂度为 O(N^2) 

1
2
3
4
5
6
7
8
9
void bubbleSort(int arr[], int size) {
    for (int i = 0; i < size-1; i++) {
        for (int j = 0; j < size-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                swap(&arr[j], &arr[j+1]); // 双重循环，操作次数为n²
            }
        }
    }
}

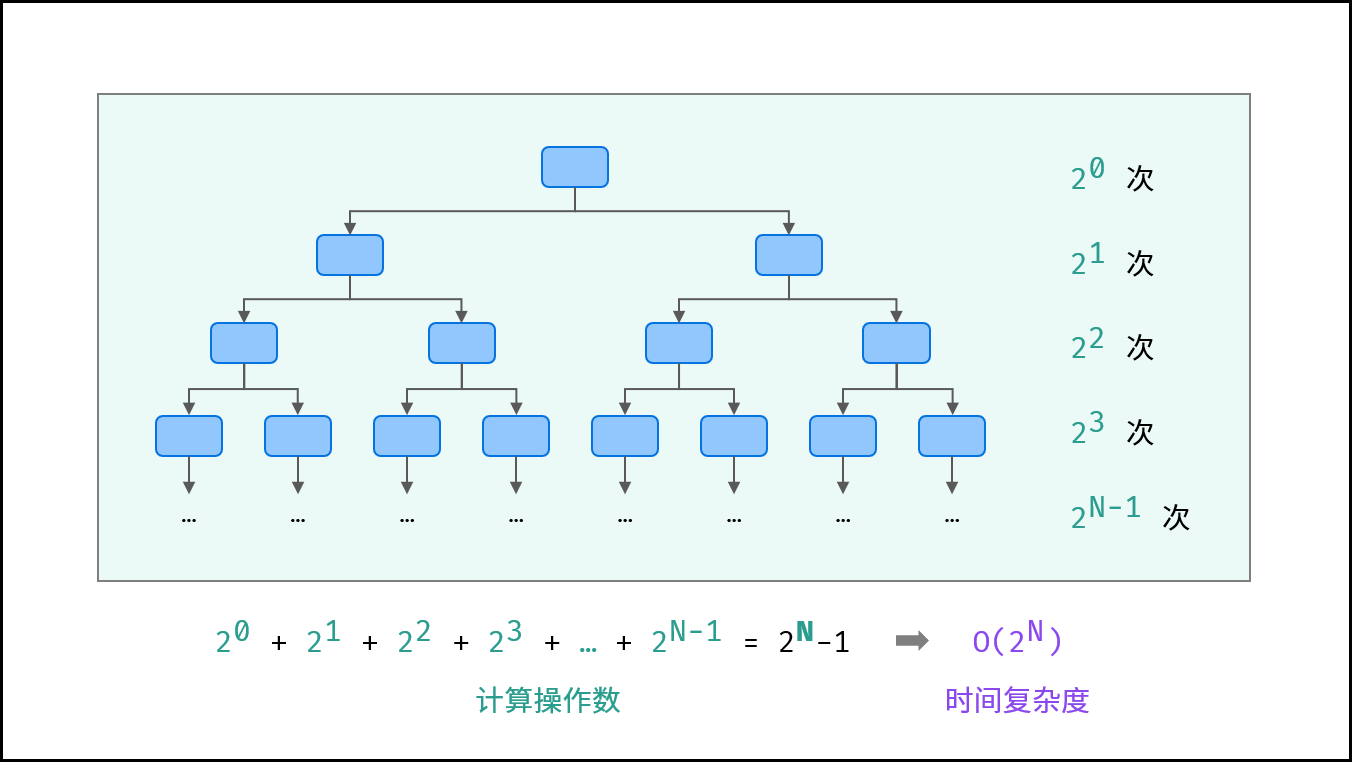
6. O(kⁿ) — 指数复杂度

特点：问题规模每增加1，计算量翻倍。
示例：斐波那契数列的递归实现。 

1
2
3
4
int fibonacci(int n) {
    if (n <= 1) return n;
    return fibonacci(n-1) + fibonacci(n-2); // 每次递归分裂为两次调用，复杂度为O(2ⁿ)
}

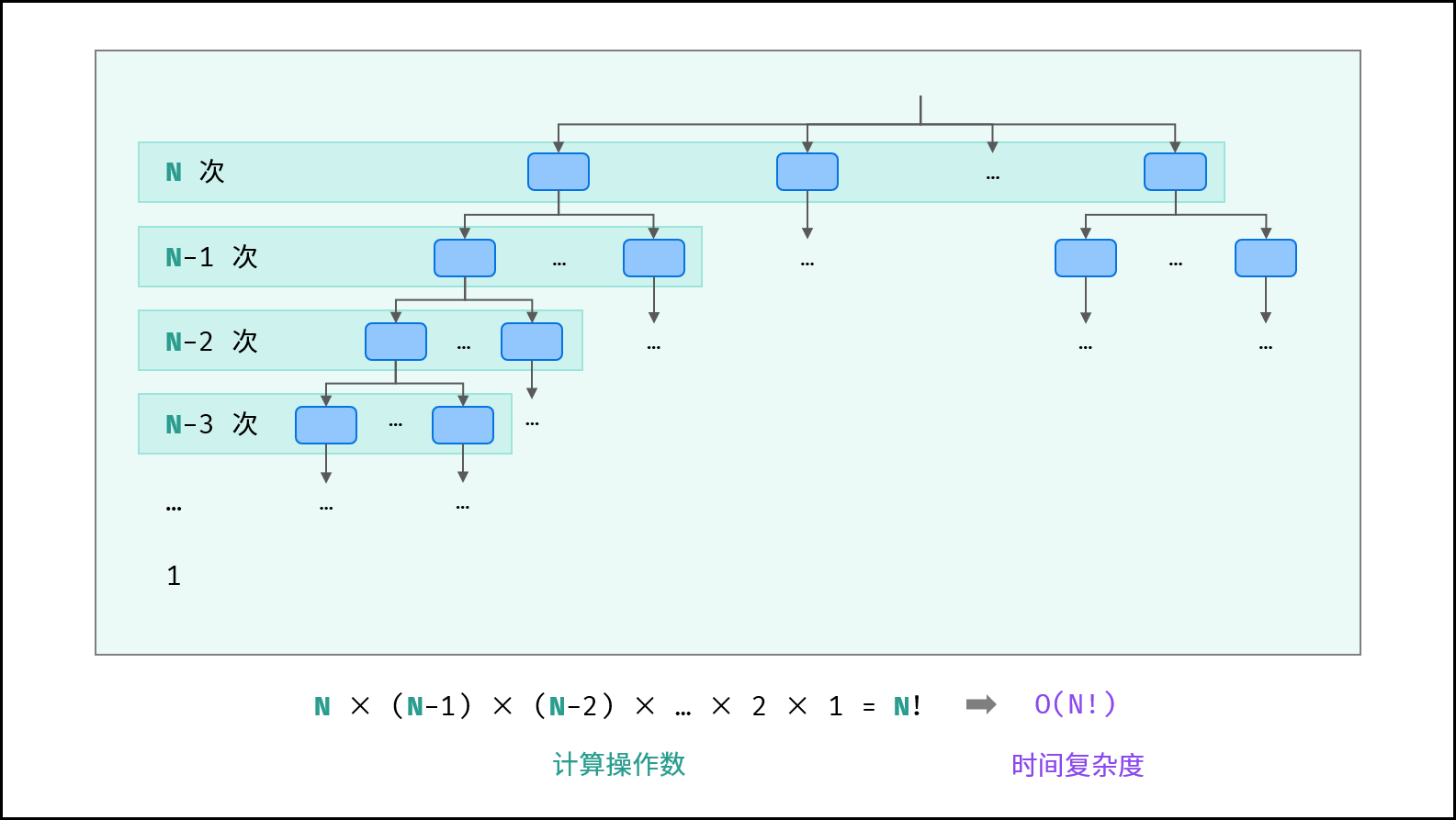
7. O(n!) — 阶乘复杂度

特点：问题规模每增加1，计算量增长为阶乘级。
示例：生成全排列，给定 NN 个互不重复的元素，求其所有可能的排列方案（递归回溯）。 

1
2
3
4
5
6
7
8
int algorithm(int N) {
    if (N <= 0) return 1;
    int count = 0;
    for (int i = 0; i < N; i++) {
        count += algorithm(N - 1);
    }
    return count;
}

时间复杂度的意义

时间复杂度不同，随着输入数据量的增加，代码运行的时间也会增加。

例如O(1)无论输入数据如何增多，代码运行时间都不变。而O(n)的运行时间和输入数据量成正比。如果时间复杂度过高，例如O(2^n)，那么在小数据情况下，代码还可以运行，一旦数据量增大，则代码的运行时间将会几何级增加。

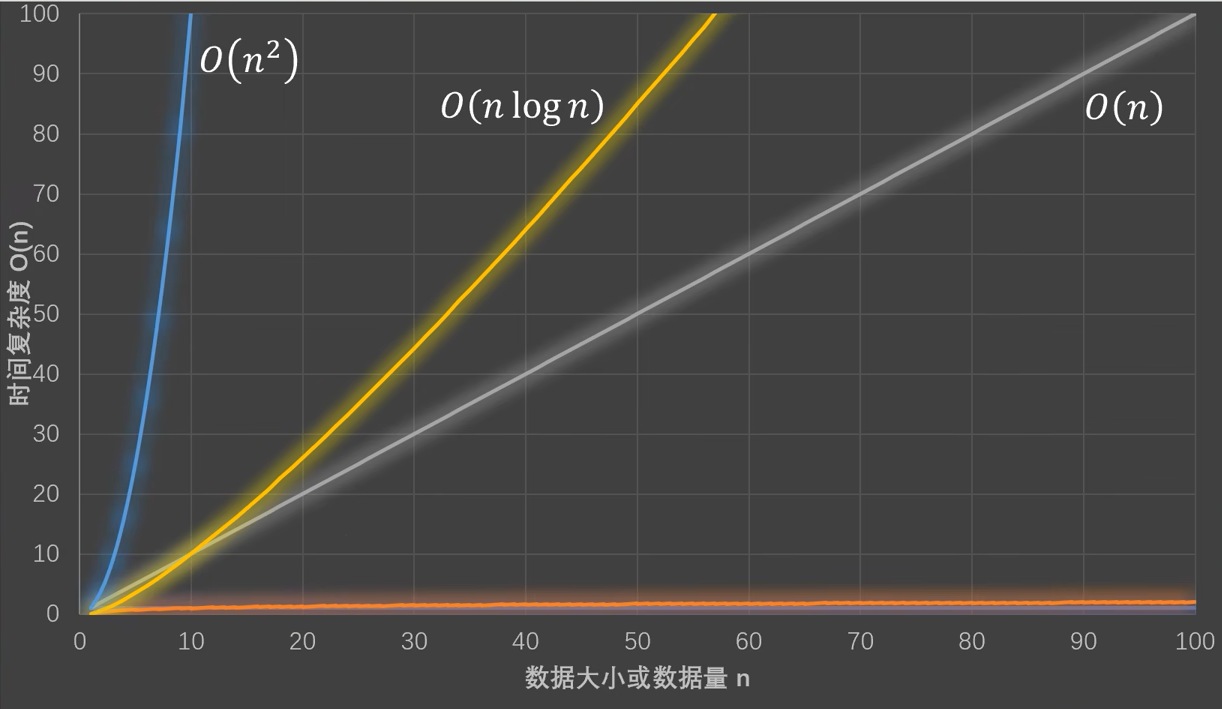
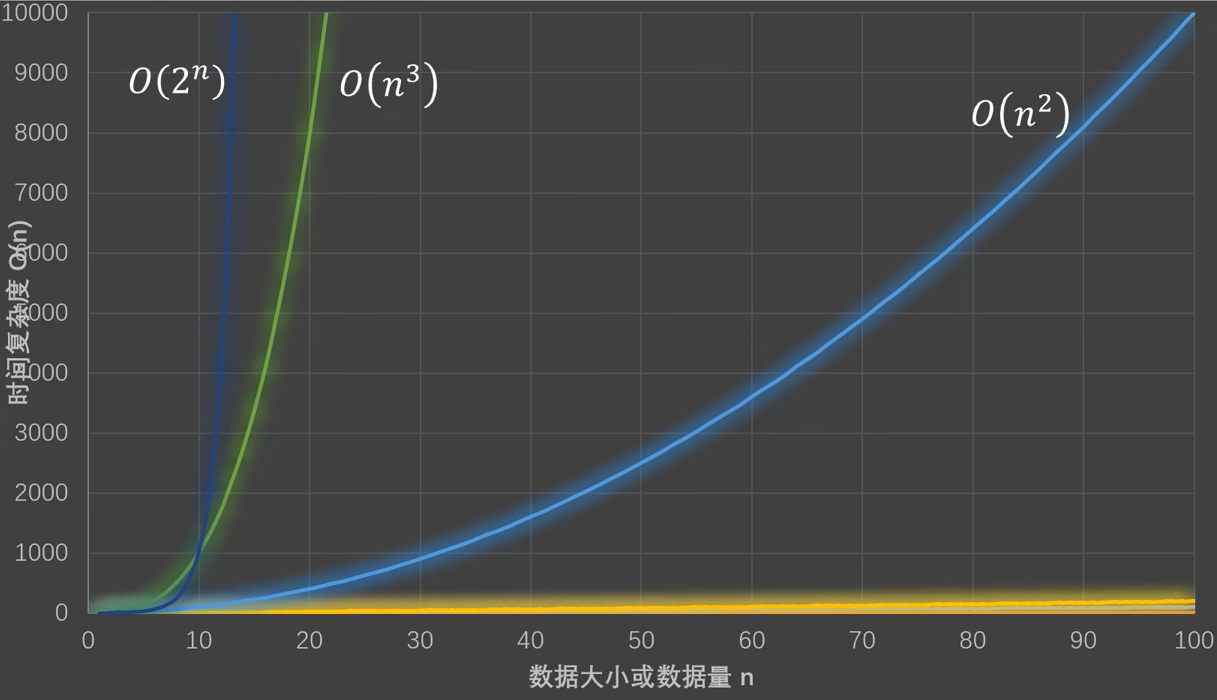
代码执行时间总结如下：

名称 时间复杂度
常数时间 O(1)
对数时间 O(log n)
线性时间 O(n)
线性对数时间 O(nlog n)
二次时间 O(n^2)
三次时间 O(n^3)
指数时间 O(2^n)

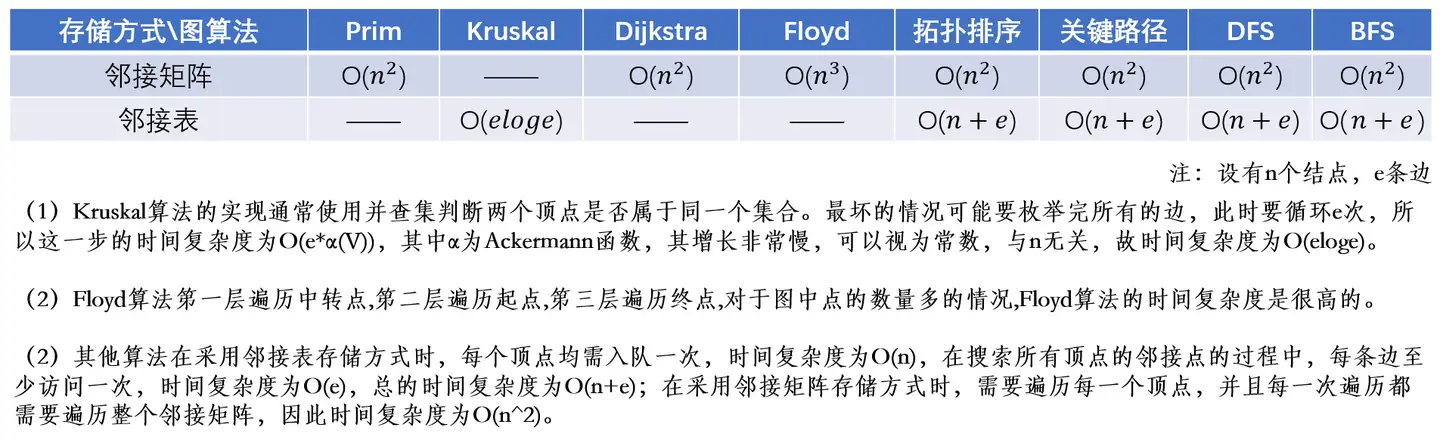
常见的时间复杂度

img

img

img

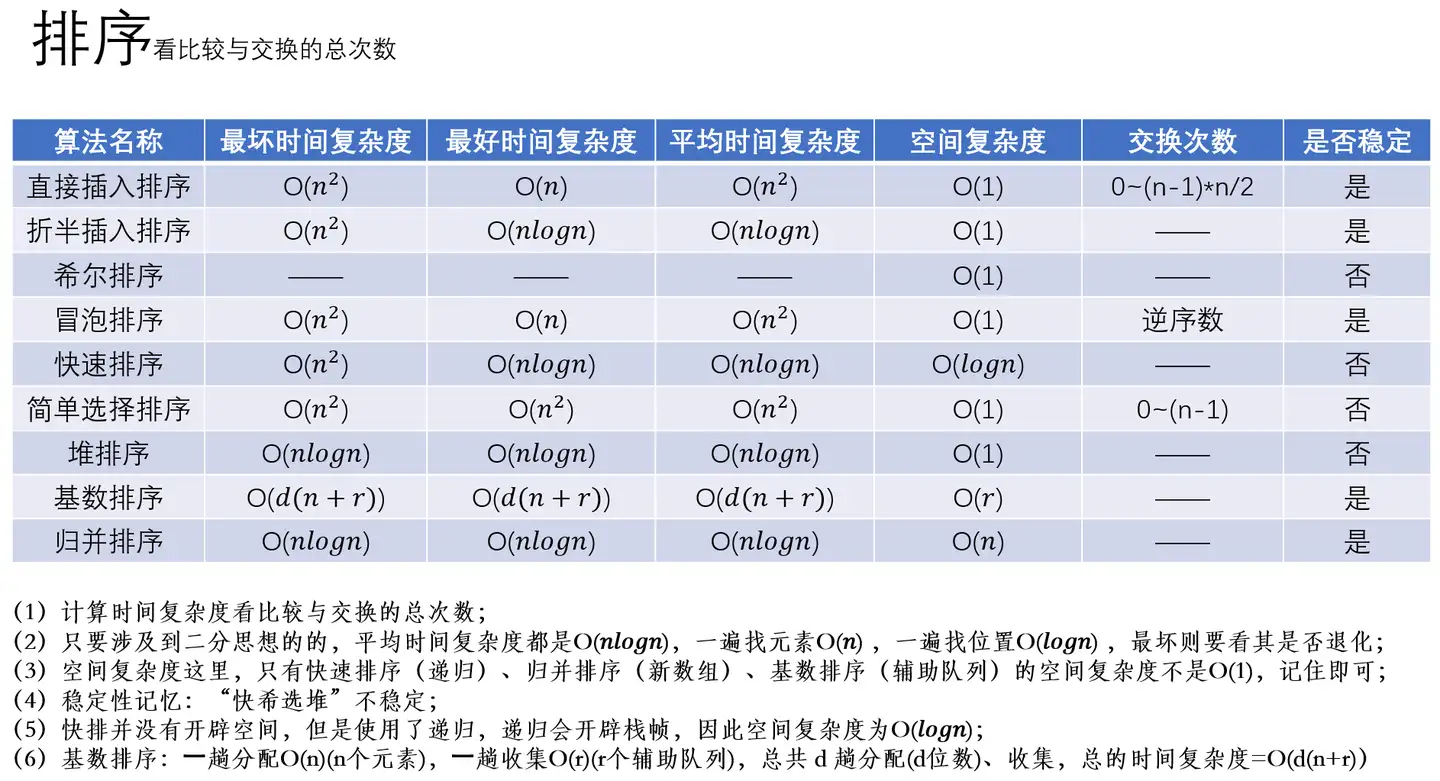
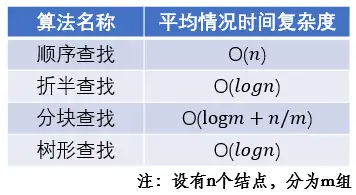
空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少字节的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

常数 O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//计算冒泡排序函数的空间复杂度
void BubbleSort(int* a, int N)
{
	assert(a);
	for (int i = 0; i < N; i++)
	{
		int exchange = 0;
		for (int j = 0; j < N - 1 - i; j++)
		{
			if (a[j]>a[j + 1])
			{
				int tmp = a[j];
				a[j] = a[j + 1];
				a[j + 1] = tmp;
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

冒泡排序函数中使用了常数个额外空间（即常数个变量），所以用大O的渐进表示法表示冒泡排序函数的空间复杂度为O(1) 。

线性 O(N)

1
2
3
4
5
//计算阶乘递归函数的空间复杂度
long long Factorial(size_t N)
{
	return N < 2 ? N : Factorial(N - 1)*N;
}

阶乘递归函数会依次调用Factorial(N),Factorial(N-1),…,Factorial(2),Factorial(1)，开辟了N个空间，所以空间复杂度为O(N) 。

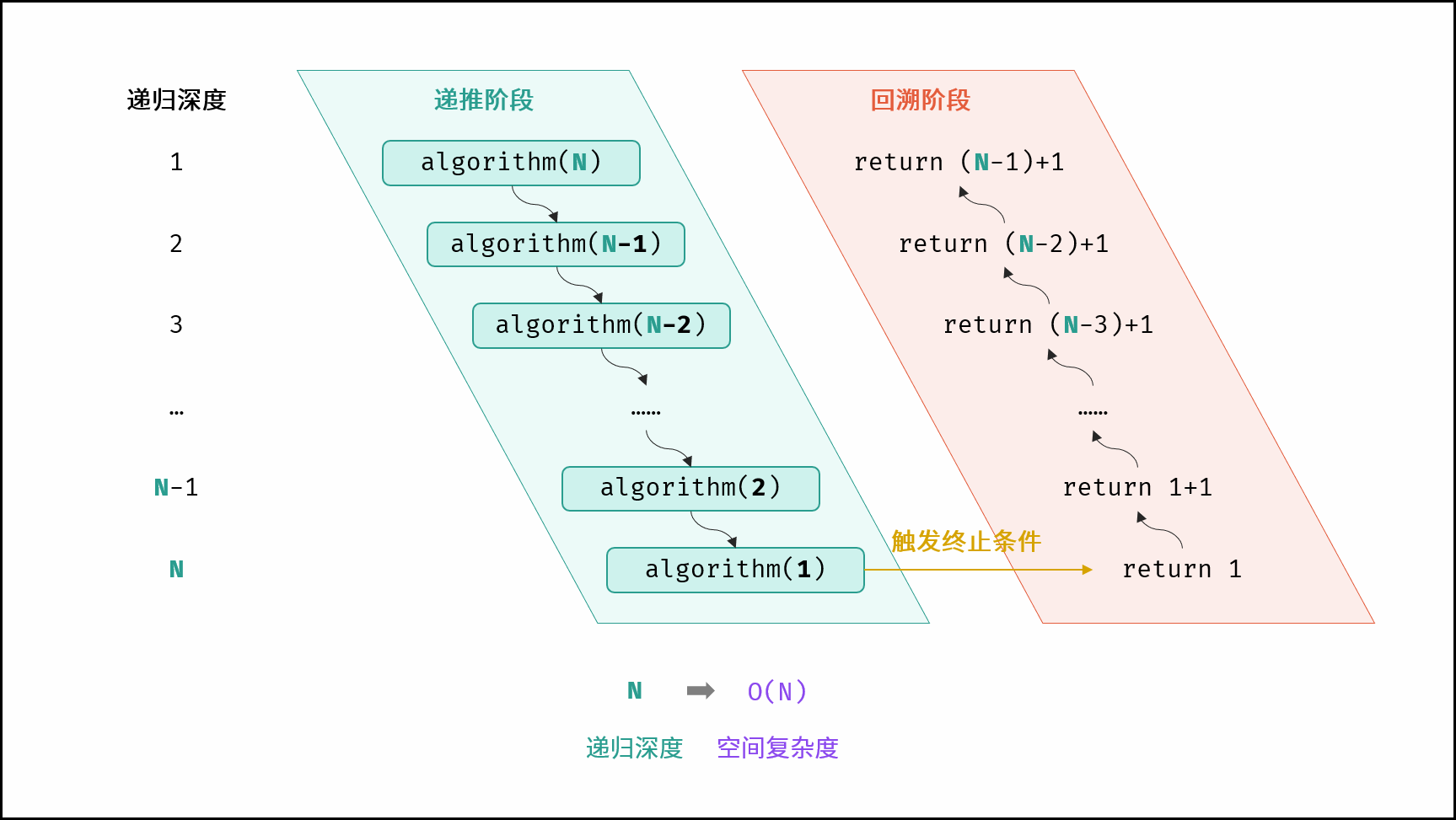
平方 O(N²)

元素数量与 N呈平方关系的任意类型集合（常见于矩阵），皆使用平方大小的空间。

  1. 递归调用栈的深度
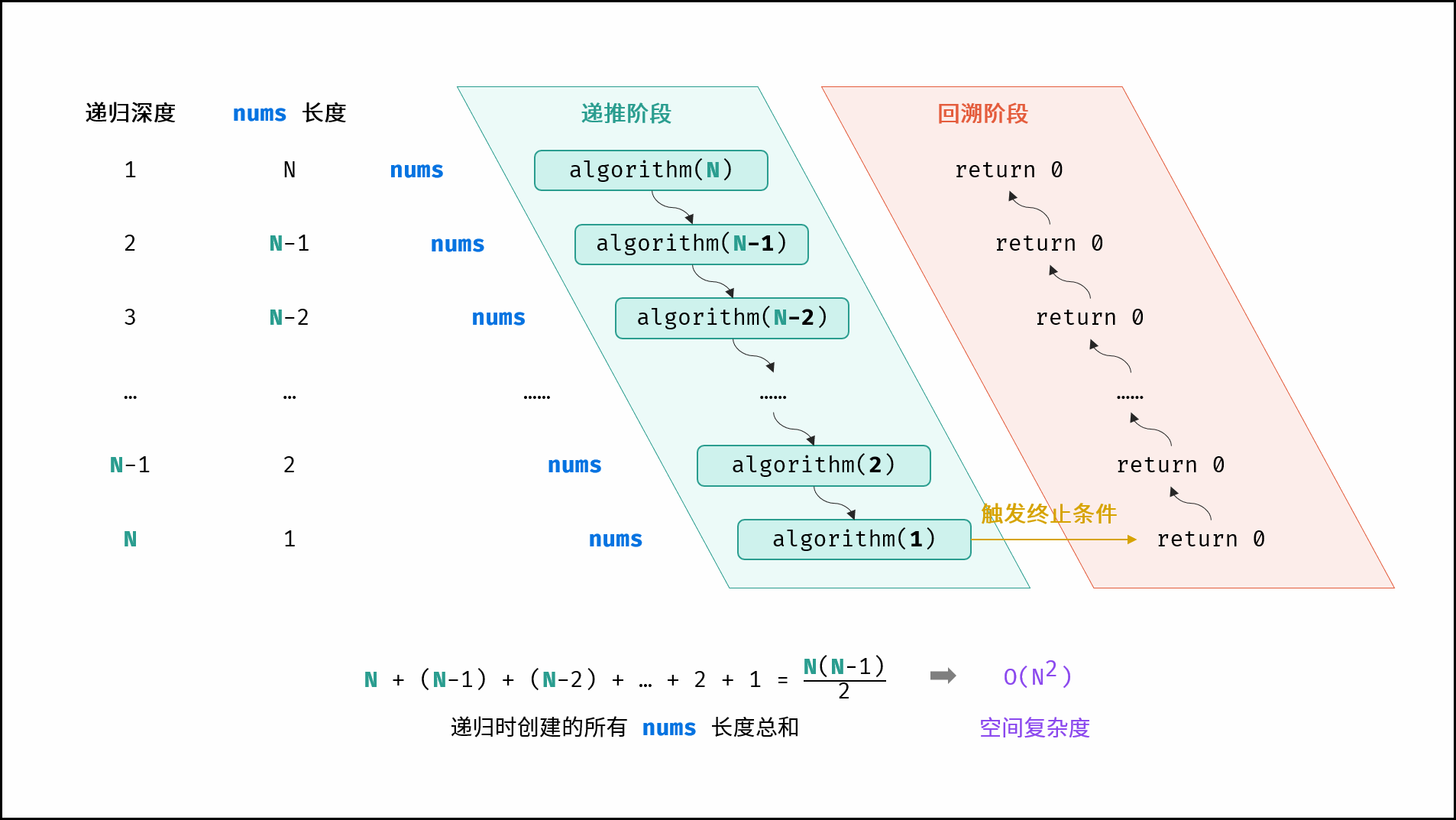
    每次递归调用参数递减 1，直到 N ≤ 0。递归深度为 N 次（例如 N=5 时调用链为 algorithm(5) → algorithm(4) → … → algorithm(0)）
  2. 每次递归的临时空间占用
    每次递归调用时，会在栈上动态创建一个大小为 N 的整型数组 int nums[N]。随着递归深度增加，数组长度的变化为 N, N-1, N-2, …, 1
  3. 空间累计计算
    总空间占用为各次递归调用中数组大小的累加：
    S(N)=N+(N−1)+(N−2)+⋯+1=2N(N+1)​
    根据大 O 表示法，简化为 ​​O(N²)​​
1
2
3
4
5
int algorithm(int N) {
    if (N <= 0) return 0;
    int nums[N];
    return algorithm(N - 1);
}

指数 O(2ᴺ)

指数阶常见于二叉树、多叉树的空间分析，例如：

  1. 满二叉树

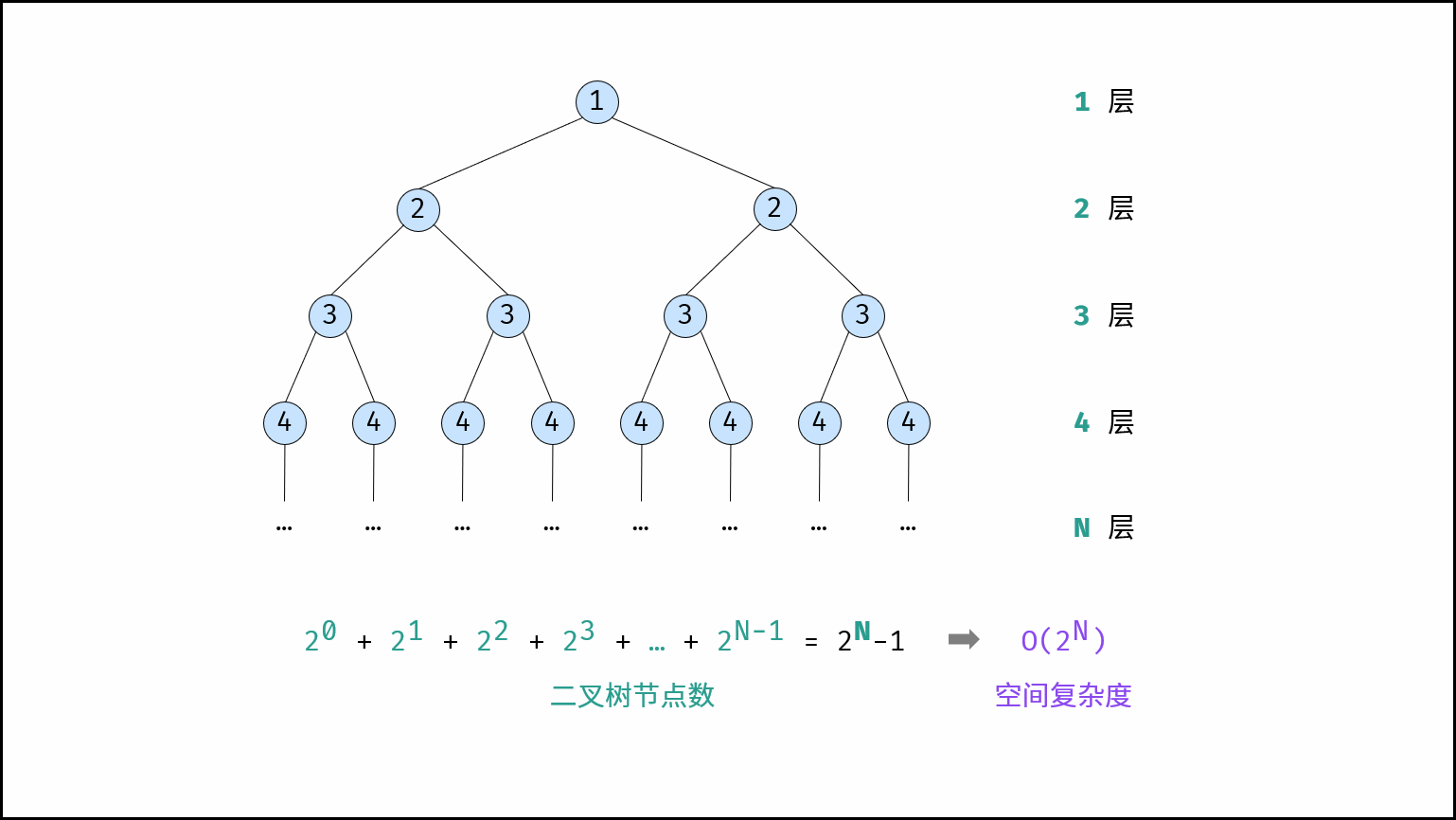
    高度为 N 的满二叉树，节点总数为 2ᴺ，空间复杂度为 O(2ᴺ)。

  2. 满 m 叉树

    高度为 N 的满 m 叉树，节点总数为 mᴺ。

    当 m 为常数时，O(mᴺ) = O(2ᴺ)（指数级增长性质相同）。

指数阶常见于二叉树、多叉树。例如，高度为 N的「满二叉树」的节点数量为 2^N，占用 O(2^N)大小的空间；同理，高度为 N的「满 m叉树」的节点数量为 m^N，占用 O(m^N)大小的空间。

对数 O(log N)

对数阶常出现于分治算法的栈帧空间累计、数据类型转换等，例如：

  • 快速排序，平均空间复杂度为 Θ(log N)，最差空间复杂度为 O(N)。
    通过应用尾递归优化，可以将快速排序的最差空间复杂度限定至 O(N)。
  • 数字转化为字符串，设某正整数为 N，则字符串的空间复杂度为 O(log N)。
    正整数 N 的位数为 log₁₀ N，即转化的字符串长度为 log₁₀ N，因此空间复杂度为 O(log N)。

注：递归算法的空间复杂度通常是递归的深度（即递归多少层）。

≡