数据结构-线性表（顺序表）

First Post:

Last Update:

Page View: loading...

线性表

说起这个问题，我们一定不陌生。打开QQ或微信，我们可以看到好友列表，打开PTA，我们能看到题目列表，打开音乐软件，我们可以看见歌曲列表，线性表在我们的生活中无处不在。线性表是怎么呈现的呢？线性表把我们在生活中需要的信息，按照顺序进行排列，使得这些信息直观、有条理，如果是按照某种顺序排列的列表，我们可以做到信息的快速检索。

img

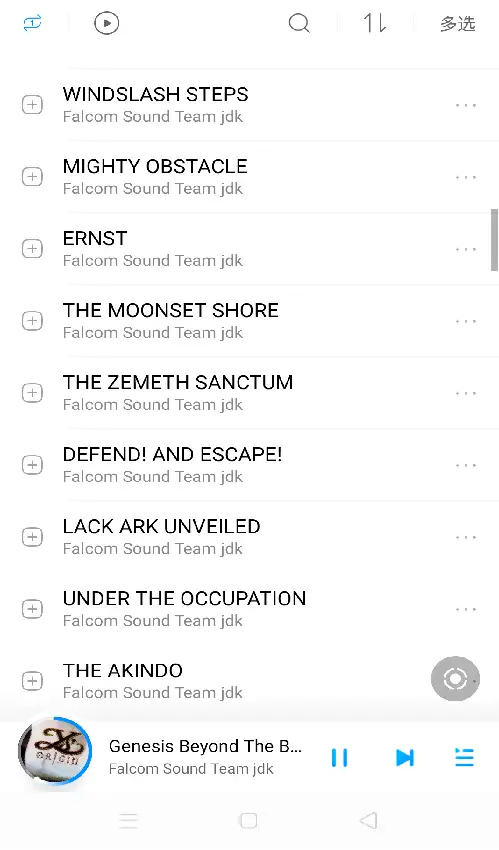
1) 线性表（线性存储结构）

线性表又称线性存储结构，是最简单的一种存储结构，专门用来存储逻辑关系为“一对一”的数据。

在一个数据集中，如果每个数据的左侧都有且仅有一个数据和它有关系，数据的右侧也有且仅有一个数据和它有关系，那么这些数据之间就是“一对一“的逻辑关系。

所谓线性表，是零个或多个数据元素的有限序列，线性表的元素具有相同的特征，数据元素之间的关系是一对一的关系。

动图封面

如上图所示，在 {1,2,3,4,5} 数据集中，每个数据的左侧都有且仅有一个数据和它紧挨着（除 1 外），右侧也有且仅有一个数据和它紧挨着（除 5 外），这些数据之间就是“一对一“的关系。

使用线性表存储具有“一对一“逻辑关系的数据，不仅可以将所有数据存储到内存中，还可以将“一对一”的逻辑关系也存储到内存中。

线性表存储数据的方案可以这样来理解，先用一根线将所有数据按照先后次序“串”起来，如下图所示：

动图封面

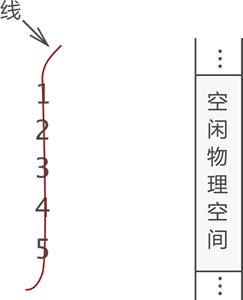
数据和“一对一”的逻辑关系

左侧是“串”起来的数据，右侧是空闲的物理空间。将这“一串儿”数据存放到物理空间中，有以下两种方法：

动图

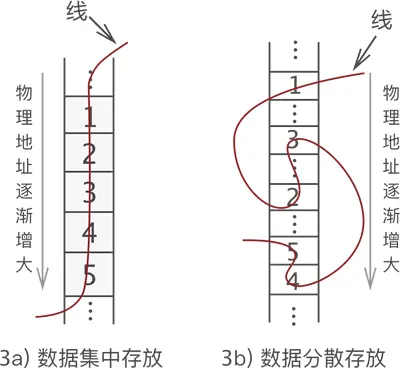
两种存储方式都可以将数据之间的关系存储起来，从线的一头开始捋，可以依次找到每个数据，且数据的前后位置没有发生改变。

像上图这样，用一根线将具有“一对一”逻辑关系的数据存储起来，这样的存储方式就称为线性表或者线性存储结构。

顺序存储结构和链式存储结构

从图 3 不难看出，线性表存储数据的实现方案有两种，分别是：

  1. 像图 3a) 那样，不破坏数据的前后次序，将它们连续存储在内存空间中，这样的存储方案称为顺序存储结构（简称顺序表）；
  2. 像图 3b) 那样，将所有数据分散存储在内存中，数据之间的逻辑关系全靠“一根线”维系，这样的存储方案称为链式存储结构（简称链表）。

也就是说，使用线性表存储数据，有两种真正可以落地的存储方案，分别是顺序表和链表。

前驱和后继

在具有“一对一“逻辑关系的数据集中，每个个体习惯称为数据元素（简称元素）。例如，图 1 显示的这组数据集中，一共有 5 个元素，分别是 1、2、3、4 和 5。

此外，很多教程中喜欢用前驱和后继来描述元素之间的前后次序：

  • 某一元素的左侧相邻元素称为该元素的“直接前驱”，此元素左侧的所有元素统称为该元素的“前驱元素”；
  • 某一元素的右侧相邻元素称为该元素的“直接后继”，此元素右侧的所有元素统称为该元素的“后继元素”；

以图 1 数据中的元素 3 来说，它的直接前驱是 2 ，此元素的前驱元素有 2 个，分别是 1 和 2；同理，此元素的直接后继是 4 ，后继元素也有 2 个，分别是 4 和 5。

动图封面

2) 顺序表（顺序存储结构）

顺序表又称顺序存储结构，是线性表的一种，专门存储逻辑关系为“一对一”的数据。

顺序表存储数据的具体实现方案是：将数据全部存储到一整块内存空间中，数据元素之间按照次序挨个存放。

举个简单的例子，将 {1,2,3,4,5} 这些数据使用顺序表存储，数据最终的存储状态如下图所示：

动图封面

线性表的抽象数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ADT List
{
    Data:
        D = {ai | 1 ≤ i ≤ n, n ≥ 0, ai 为 ElemType 类型}
    Relation：
        R = { <ai,ai+1> | ai,ai+1 ∈ D, i = 1, i ∈ (0,n)}
    Operation:
        InitList(&L);    //初始化，建立一个空的线性表L
        MakeList(&L);    //建立线性表，向表中存入数据
        ListEmpty(*L);    //空表判断，是则返回true,否则返回false
        DestroyList(&L);    //清除操作，清空线性表的元素
        GetElem(L,i,&e);    //获取线性表的元素，将线性表L的第i个元素的值返回给e
        LocateElem(L,e);    //按值查找元素，在线性表L中查找与e元素相等的元素，查找成功返回对应的序号，查找失败则返回0
        ListInsert(&L,i,e);    //插入操作，在线性表L的第i个位置插入元素e
        ListDelete(&L,i,&e);    //删除操作，删除线性表L中的第i个位置的元素，并将其用e返回
        ListLength(L);    //计算表长，返回线性表L的元素个数
        DispList(L);    //输出线性表，当线性表不为空表时，按顺序输出表中的每一个元素
}

顺序表的建立

使用顺序表存储数据，除了存储数据本身的值以外，通常还会记录以下两样数据：

  • 顺序表的最大存储容量：顺序表最多可以存储的数据个数；
  • 顺序表的长度：当前顺序表中存储的数据个数。

C 语言中，可以定义一个结构体来表示顺序表：

1
2
3
4
5
typedef struct{
    int * head; //定义一个名为head的长度不确定的数组，也叫“动态数组”
    int length; //记录当前顺序表的长度
    int size; //记录顺序表的存储容量
}Table;

尝试建立一个顺序表，例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#define Size 5 //对Size进行宏定义，表示顺序表的最大容量
void initTable(Table * t) {
    //构造一个空的顺序表，动态申请存储空间
    t->head = (int*)malloc(Size * sizeof(int)); //申请内存空间
    //如果申请失败，作出提示并直接退出程序
    if (!t->head)
    {
        printf("初始化失败");
        exit(0);
    }
    //空表的长度初始化为0
    t->length = 0;
    //空表的初始存储空间为Size
    t->size = Size;
}

如上所示，整个建立顺序表的过程都封装在一个函数中，建好的顺序表可以存储 5 个逻辑关系为“一对一”的整数。

在顺序表的实现中，t->head 是一个指向动态数组基地址的指针，其核心作用是为顺序表提供存储数据的连续内存空间。以下是具体解析：

1. t->head 的定义与作用

• 定义：
t->head 是顺序表结构体中的一个成员变量，通常声明为动态数组的起始地址指针。例如在 C 语言中，顺序表的结构体定义如下：

1
2
3
4
5
typedef struct {
    int *head;  // 动态数组基地址
    int length; // 当前元素个数
    int size;   // 总存储容量
} Table;

顺序表的使用

通过调用 initTable() 函数，就可以成功地创建一个顺序表，还可以往顺序表中存储一些元素。

例如，将 {1,2,3,4,5} 存储到顺序表中，实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <stdio.h>
#include <stdlib.h>
#define Size 5 //对Size进行宏定义，表示顺序表的最大容量
typedef struct{
    int* head;
    int length;
    int size;
}Table;


void initTable(Table * t) {
    //构造一个空的顺序表，动态申请存储空间
    t->head = (int*)malloc(Size * sizeof(int));
    //如果申请失败，作出提示并直接退出程序
    if (!t->head) //无头（申请失败）
    {
        printf("初始化失败");
        exit(0);
    }
    //空表的长度初始化为0
    t->length = 0; //t->length：当前元素个数
    //空表的初始存储空间为Size
    t->size = Size; //t->size：总存储容量
}
//输出顺序表中元素的函数


void displayTable(Table t) {
    int i;
    for (i = 0; i < t.length; i++) {
        printf("%d ", t.head[i]);
    }
    printf("\n");
}


int main() {
    int i;
    Table t = { NULL,0,0 };
    initTable(&t);
    //向顺序表中添加{1,2,3,4,5}
    for (i = 1; i <= Size; i++) {
        t.head[i - 1] = i;
        t.length++;
    }
    printf("顺序表中存储的元素分别是：\n");
    displayTable(t);
    free(t.head);//释放申请的堆内存
    return 0;
}

程序运行结果如下：

顺序表中存储的元素分别是： 1 2 3 4 5

3) 顺序表的基本操作

我们学习了顺序表及初始化的过程，本节学习有关顺序表的一些基本操作，以及如何使用 C 语言实现它们。

顺序表插入元素

向已有顺序表中插入数据元素，根据插入位置的不同，可分为以下 3 种情况：

  1. 插入到顺序表的表头；
  2. 在表的中间位置插入元素；
  3. 尾随顺序表中已有元素，作为顺序表中的最后一个元素；

虽然数据元素插入顺序表中的位置有所不同，但是都使用的是同一种方式去解决，即：通过遍历，找到数据元素要插入的位置，然后做如下两步工作：

  • 将要插入位置元素以及后续的元素整体向后移动一个位置；
  • 将元素放到腾出来的位置上；

例如，在 {1,2,3,4,5} 的第 3 个位置上插入元素 6，实现过程如下：

  • 遍历至顺序表存储第 3 个数据元素的位置

动图封面

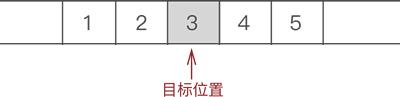
  • 将元素 3、4 和 5 整体向后移动一个位置

动图封面

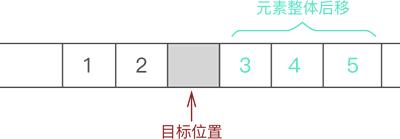
  • 将新元素 6 放入腾出的位置

动图封面

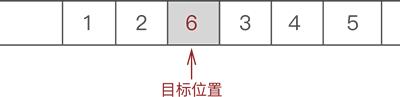
因此，顺序表插入数据元素的 C 语言实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//插入函数，其中，elem为插入的元素，add为插入到顺序表的位置
void insertTable(Table* t, int elem, int add)
{
    int i;
    
    
    //如果插入元素位置(add)比整张表的长度+1(t->length + 1)还大（如果相等，是尾随的情况），或者插入的位置本身不存在，程序作为提示并自动退出
    if (add > t->length + 1 || add < 1) {
        printf("插入位置有问题\n");
        return;
    }
    
    
    //做插入操作时，首先需要看顺序表是否有多余的存储空间提供给插入的元素，有就是(t->length < t->size)，如果没有就是(t->length == t->size)，需要申请
    if (t->length == t->size) {
        t->head = (int*)realloc(t->head, (t->size + 1) * sizeof(int));
        //重新分配内存，动态数组额外申请更多物理空间
        if (!t->head) {
            printf("存储分配失败\n");
            return;
        }
        t->size += 1;
    }
    
    
    //插入操作，需要将自插入位置之后的所有元素(从t->length - 1倒数到add - 1)全部后移一位
    for (i = t->length - 1; i >= add - 1; i--) {
        t->head[i + 1] = t->head[i];
    }
    
    //后移完成后，直接插入元素
    t->head[add - 1] = elem;
    t->length++;
}

注意，动态数组额外申请更多物理空间使用的是 realloc 函数。此外在实现元素整体后移的过程中，目标位置其实是有数据的，还是 3，只是下一步新插入元素时会把旧元素直接覆盖。

顺序表删除元素

从顺序表中删除指定元素，实现起来非常简单，只需找到目标元素，并将其后续所有元素整体前移 1 个位置即可。

后续元素整体前移一个位置，会直接将目标元素删除，可间接实现删除元素的目的。

例如，从 {1,2,3,4,5} 中删除元素 3 的过程如图 4 所示：

动图封面

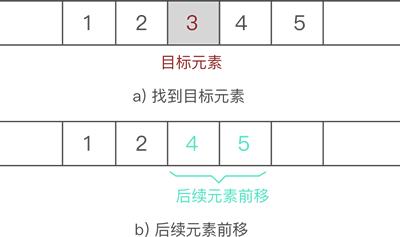
因此，顺序表删除元素的 C 语言实现代码为：

1
2
3
4
5
6
7
8
9
10
11
12
void delTable(Table* t, int add) {
    int i;
    if (add > t->length || add < 1) {  //删除元素位置大于表长或小于0
        printf("被删除元素的位置有误\n");
        return;
    }
    //删除操作
    for (i = add; i < t->length; i++) {
        t->head[i - 1] = t->head[i];
    }
    t->length--;//表长减短
}

顺序表查找元素

顺序表中查找目标元素，可以使用多种查找算法实现，比如说二分查找算法、插值查找算法等。

这里，我们选择顺序查找算法，具体实现代码为：

1
2
3
4
5
6
7
8
9
//查找函数，其中，elem表示要查找的数据元素的值
int selectTable(table t,int elem){
    for (int i=0; i<t.length; i++) {
        if (t.head[i]==elem) {
            return i+1;
        }
    }
    return -1;//如果查找失败，返回-1
}

顺序表更改元素

顺序表更改元素的实现过程是：

  1. 找到目标元素；
  2. 直接修改该元素的值；

顺序表更改元素的 C 语言实现代码为：

1
2
3
4
5
6
7
8
void amendTable(Table* t, int elem, int newElem) {
    int add = selectTable(*t, elem);
    if (add == -1) {
        printf("顺序表中没有找到目标元素\n");
        return;
    }
    t->head[add - 1] = newElem;
}

关于 t->head,t->length和 t->size

• 物理存储管理：
t->head 指向通过 malloc 或 realloc 动态申请的内存块的首地址。顺序表中的所有元素按逻辑顺序连续存储在这段内存中。

• 操作接口：
通过 t->head 可直接访问顺序表的元素，例如：
• 插入：t->head[add-1] = elem 将元素写入指定位置。
• 遍历：通过 t->head[i] 访问第 i 个元素。

顺序表初始化时，t->head 被赋予动态分配的内存地址。例如： 

1
2
3
4
5
void initTable(Table *t) {
    t->head = (int*)malloc(Size * sizeof(int));  // 申请初始内存
    t->length = 0;
    t->size = Size;
}

若内存分配失败，t->head 会指向 NULL，此时需进行错误处理。

所有对顺序表元素的增删查改均通过 t->head 实现：
• 插入元素：将后续元素右移后，直接通过 t->head[add-1] 写入新值。
• 删除元素：左移覆盖目标元素后，通过 t->head 重新定位后续元素。

t->head 是顺序表实现中动态内存管理的核心，它指向存储数据的连续内存块，并通过指针操作支持元素的增删查改。

在顺序表的实现中，t->length和t->size是两个关键字段，它们的含义及设计逻辑如下：

1. t->length：当前元素个数

• 定义：表示顺序表中实际存储的有效元素数量，即当前表内数据的逻辑长度。
• 作用：
• 控制插入/删除操作的合法性（例如插入位置不能超过length+1，删除位置不能超过length）。
• 遍历时确定元素范围（从下标0到length-1）。
• 示例：若顺序表存储{1,2,3}，则length=3。

2. t->size：总存储容量

• 定义：表示顺序表已申请的内存空间能容纳的最大元素数量，即物理存储容量。
• 作用：
• 判断是否需要扩容（当length == size时，表已满需扩展内存）。
• 动态调整内存时记录当前分配的空间上限。
• 示例：若初始分配容量为size=5，插入5个元素后length=5，此时需扩容才能继续插入。

3. 两者的区别与联系

字段 意义 操作触发条件 命名逻辑
length 实际元素个数（动态变化） 插入时位置需满足1 ≤ add ≤ length+1 直观体现“逻辑长度”，类似数组的size()
size 最大容量（静态/动态） 扩容条件为length == size 体现“物理容量上限”，类似容器的capacity()

  1. 逻辑与物理分离：
    • length关注数据逻辑层面的使用情况，size关注物理内存的管理，两者分离便于维护动态内存。

  2. 操作安全性：
    • 通过length限制插入/删除位置，避免越界访问；通过size判断内存是否耗尽，防止溢出。

  3. 动态扩容机制：
    • 当length达到size时，触发realloc扩展内存（例如每次扩容固定步长或按倍数增长），保证数据连续性。

    插入函数中：

1
2
3
4
5
6
7
8
if (add > t->length + 1 || add < 1) {
    printf("插入位置有问题\n");
    return;
}
if (t->length == t->size) {
    t->head = (int*)realloc(t->head, (t->size + 1) * sizeof(int));
    // 扩容逻辑...
}

• add > t->length + 1：确保插入位置不超过逻辑长度的下一个合法位置（如length=3时，允许插入到第4位，但不可到第5位）。
• t->length == t->size：触发扩容的条件，保证物理空间始终足够容纳逻辑元素。

t->length和t->size是顺序表实现中动态内存管理与逻辑操作控制的核心字段。通过两者的协同，既能高效利用内存，又能确保数据操作的合法性。

其他操作的实现

逆序

1
2
3
4
5
6
7
8
9
void reverseTable(Table* t) {
    if (t->length <= 1) return; // 空表或单元素表无需处理
    
    for (int i = 0; i < t->length / 2; i++) {
        int temp = t->head[i];
        t->head[i] = t->head[t->length - 1 - i];
        t->head[t->length - 1 - i] = temp;
    }
}

输出表长

1
2
3
int ListLength(Table* t) {
    return L->length; // 直接返回顺序表的当前长度
}

删除全表

1
2
3
4
5
6
7
void SeqListDestory(Table* t) {
    assert(t);  // 确保传入的指针非空
    free(t->head);  // 释放动态数组内存
    t->head = NULL;  // 指针置空
    t->size = 0;  // 容量归零
    t->length = 0;  // 元素个数归零
}

完整代码实现

以下是一个完整的顺序表操作示例代码，包含初始化、插入、删除、查找、修改、逆序、销毁等操作，并在main函数中展示了具体调用逻辑：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define INIT_SIZE 5  // 初始容量

typedef struct {
    int* head;    // 动态数组基地址
    int length;   // 当前元素个数
    int size;     // 总存储容量
} Table;

// 初始化顺序表
void initTable(Table* t) {
    t->head = (int*)malloc(INIT_SIZE * sizeof(int));
    if (!t->head) {
        printf("内存分配失败\n");
        exit(EXIT_FAILURE);
    }
    t->length = 0;
    t->size = INIT_SIZE;
}

// 插入元素（位置从1开始）
void insertTable(Table* t, int elem, int pos) {
    if (pos < 1 || pos > t->length + 1) {
        printf("非法插入位置: %d\n", pos);
        return;
    }
    
    // 容量检查与扩容
    if (t->length == t->size) {
        int new_size = t->size * 2;  // 容量翻倍
        int* new_head = (int*)realloc(t->head, new_size * sizeof(int));
        if (!new_head) {
            printf("扩容失败\n");
            return;
        }
        t->head = new_head;
        t->size = new_size;
        printf("已扩容至 %d\n", new_size);
    }

    // 元素后移
    for (int i = t->length; i >= pos; i--) {
        t->head[i] = t->head[i - 1];
    }
    
    t->head[pos - 1] = elem;
    t->length++;
}

// 删除元素（位置从1开始）
void delTable(Table* t, int pos) {
    if (pos < 1 || pos > t->length) {
        printf("非法删除位置: %d\n", pos);
        return;
    }
    
    // 元素前移覆盖
    for (int i = pos; i < t->length; i++) {
        t->head[i - 1] = t->head[i];
    }
    t->length--;
}

// 查找元素（返回位置，从1开始）
int selectTable(Table* t, int elem) {
    for (int i = 0; i < t->length; i++) {
        if (t->head[i] == elem) {
            return i + 1;// 返回元素位置
        }
    }
    return -1;  // 未找到
}

// 修改元素值
void amendTable(Table* t, int old_elem, int new_elem) {
    int pos = selectTable(t, old_elem); // 查找元素
    if (pos == -1) {
        printf("元素 %d 不存在\n", old_elem);
        return;
    }
    t->head[pos - 1] = new_elem;
}

// 逆序顺序表
void reverseTable(Table* t) {
    for (int i = 0; i < t->length / 2; i++) {
        int temp = t->head[i];
        t->head[i] = t->head[t->length - 1 - i];
        t->head[t->length - 1 - i] = temp;
    }
}

// 销毁顺序表
void destroyTable(Table* t) {
    free(t->head);
    t->head = NULL;
    t->length = 0;
    t->size = 0;
}

// 打印顺序表
void displayTable(Table* t) {
    printf("[当前表长: %d, 总容量: %d]\n", t->length, t->size);
    for (int i = 0; i < t->length; i++) {
        printf("%d ", t->head[i]);
    }
    printf("\n\n");
}

int main() {
    Table my_table; //声明一个名为 my_table 的变量，其类型为 Table 结构体
    
    // 1. 初始化
    initTable(&my_table);
    //&my_table的作用是将结构体的地址传递给函数，使函数能通过指针直接修改原始变量
    printf("=== 初始化顺序表 ===\n");
    displayTable(&my_table);

    // 2. 插入初始元素
    for (int i = 1; i <= 5; i++) {
        insertTable(&my_table, i, i);
    }
    printf("=== 插入5个元素 ===\n");
    displayTable(&my_table);

    // 3. 测试扩容插入
    insertTable(&my_table, 6, 3);  // 在第3位插入6
    printf("=== 插入第6个元素触发扩容 ===\n");
    displayTable(&my_table);

    // 4. 删除元素
    delTable(&my_table, 2);  // 删除第2个元素
    printf("=== 删除第2个元素 ===\n");
    displayTable(&my_table);

    // 5. 查找元素
    int target = 6;
    int pos = selectTable(&my_table, target);
    printf("=== 查找元素 %d ===\n", target);
    if (pos != -1) {
        printf("元素 %d 位于第 %d 位\n", target, pos);
    } else {
        printf("元素不存在\n");
    }

    // 6. 修改元素
    amendTable(&my_table, 6, 66);
    printf("=== 修改元素 6 → 66 ===\n");
    displayTable(&my_table);

    // 7. 逆序操作
    reverseTable(&my_table);
    printf("=== 逆序顺序表 ===\n");
    displayTable(&my_table);

    // 8. 销毁顺序表
    destroyTable(&my_table);
    printf("=== 销毁后的状态 ===\n");
    printf("指针状态: %s\n", (my_table.head == NULL) ? "已释放" : "未释放");
    
    return 0;
}

关键调用逻辑说明：

  1. 初始化顺序表 

    1
    initTable(&my_table);

    • 创建空表，初始容量为5
    • 时间复杂度：O(1)

  2. 批量插入元素

    1
    2
    3
    for (int i = 1; i <= 5; i++) {
        insertTable(&my_table, i, i);
    }

    • 插入5个元素填满初始容量
    • 时间复杂度：O(n)

  3. 触发扩容插入 

    1
    insertTable(&my_table, 6, 3);

    • 当插入第6个元素时触发动态扩容（容量翻倍为10）
    • 时间复杂度：O(n)

  4. 删除元素 

    1
    delTable(&my_table, 2);

    • 删除第2个元素（值为2），后续元素前移
    • 时间复杂度：O(n)

  5. 元素查找 

    1
    selectTable(&my_table, target);

    • 使用顺序查找，返回元素位置
    • 时间复杂度：O(n)

  6. 逆序操作

    1
    reverseTable(&my_table);

    • 通过对称交换实现逆序
    • 时间复杂度：O(n)

  7. 销毁顺序表 

    1
    destroyTable(&my_table);

    • 释放动态内存并将指针置空
    • 防止内存泄漏的关键操作

执行结果示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
=== 初始化顺序表 ===
[当前表长: 0, 总容量: 5]


=== 插入5个元素 ===
[当前表长: 5, 总容量: 5]
1 2 3 4 5 

已扩容至 10
=== 插入第6个元素触发扩容 ===
[当前表长: 6, 总容量: 10]
1 2 6 3 4 5 

=== 删除第2个元素 ===
[当前表长: 5, 总容量: 10]
1 6 3 4 5 

=== 查找元素 6 ===
元素 6 位于第 2 位
=== 修改元素 6 → 66 ===
[当前表长: 5, 总容量: 10]
1 66 3 4 5 

=== 逆序顺序表 ===
[当前表长: 5, 总容量: 10]
5 4 3 66 1 

=== 销毁后的状态 ===
指针状态: 已释放

复杂度对比：

操作 最好情况 最坏情况 平均情况
插入 O(1) O(n) O(n)
删除 O(1) O(n) O(n)
查找 O(1) O(n) O(n)
逆序 - O(n) O(n)
初始化 O(1) O(1) O(1)

​ 首先是插入操作，插入操作时间复杂度最小的情况是，当元素要插入到最后一个位置时，你就不需要移动任何元素即可实现，只需要将需要插入的元素插在表的末端即可，时间复杂度O(1)，最费时的操作就是插入的元素要放在表头，那我们就需要把表中的所有元素都移动了,时间复杂度为O(n)。

​ 删除操作也如此，当我们要删除最后一个元素，也不需要移动顺序表，而删除第一个元素时需要移动整个表。我们知道，在实际的操作中，删除表中的任何一个位置需要被插入删除的可能性是相同的，因此从平均角度来分析，移动表的平均次数为 (n - 1) / 2，时间复杂度为O(n)。
​ 因此我们可以看出，顺序表在插入、删除操作时是比较费时间的，然而其他的基本操作例如初始化、建表或者销毁，时间复杂度都是O(1)，因此我们在使用顺序表的时候，要尽量让表保持不变，而是多多使用顺序表的存储和随机提取等优点。

优缺点分析

顺序表主要有如下一些优点：

  1. 顺序表进行随机提取元素的效率较高，能够快速存储、提取元素；
  2. 建表时无需对表中元素的逻辑关系进行描述，各元素在存储地址上是连续的；
  3. 对于CPU，顺序表的高速缓存效率更高，且CPU流水线也不会总是被打断。

顺序表主要有如下一些缺点：

  1. 申请顺序表时，顺序表存储元素的上限是固定的，这就导致了存在溢出的可能性；
  2. 插入、删除元素时，时间复杂度较大，需要大范围移动表中的元素；
  3. 由于我们在很多情况下无法预知需要存储多少元素，因此容易导致内存碎片的现象，即申请了空间却没有充分利用。

关于链表再新开一个页面

≡