Mover方法笔记

MOVER方法详解：原理、过程与实例分析

---

一、MOVER方法的基本原理

MOVER（Method of Variance Estimates Recovery，方差重估计法）是一种用于构造两参数差值或比值置信区间的统计学方法，由Newcombe于1998年首次提出，后由Zou等学者系统发展。其核心思想是通过重构参数的左右方差，解决传统方法（如Delta法、Fieller法）在数据偏态分布或小样本场景下覆盖率不准确的问题。

方差分解：将置信区间信息转化为“左/右方差基础”

MOVER方法的第一步是分解参数的置信区间，将其上下限与点估计值的距离分别定义为左方差基础（$d_{i1}$）和右方差基础（$d_{i2}$）：

$$
d_{i1} = \hat{\theta}_i - \hat{l}i ，左方差基础=参数点估计值-置信区间下限
$$
$$
d{i2} = \hat{u}_i - \hat{\theta}_i ，右方差基础=置信区间上限-参数点估计值
$$

• $\hat{\theta}_i$ 是参数的点估计值（如均值、率比等）
• $\hat{l}_i$ 和 $\hat{u}_i$ 是该参数的置信区间下限和上限（如95% CI）
• $d_{i1}$ 表示点估计值到置信下限的距离（“左方差基础”）
• $d_{i2}$ 表示点估计值到置信上限的距离（“右方差基础”）

为什么需要分解方差？

• 传统方法假设参数服从对称分布（如正态分布），但现实中许多统计量（如比值、率比）可能呈现偏态分布。
• MOVER方法通过分解左右方差能够更灵活地处理非对称数据，提高置信区间的准确性。

2. 方差重估计：利用置信区间反推方差

在分解出 $d_{i1}$ 和 $d_{i2}$ 后，MOVER方法进一步利用置信区间的宽度反推方差：

$$
\hat{\sigma}{i1}^2 = \frac{\hat{d}{i1}^2}{z_{\alpha/2}^2}
$$
$$
\hat{\sigma}{i2}^2 = \frac{\hat{d}{i2}^2}{z_{\alpha/2}^2}
$$

基于置信下限计算的“左方差” = 左方差基础的平方 / 标准正态分布的 $1 - \alpha/2$ 分位数的平方
基于置信上限计算的“右方差” = 右方差基础的平方 / 标准正态分布的 $1 - \alpha/2$ 分位数的平方

• $z_{\alpha/2}$ 是标准正态分布的 $1 - \alpha/2$ 分位数（如95% CI对应 $z_{0.025} \approx 1.96$）。

• $\hat{\sigma}_{i1}^2$ 是基于置信下限计算的“左方差”。

• $\hat{\sigma}_{i2}^2$ 是基于置信上限计算的“右方差”。

• 传统方法通常使用单一方差估计（如样本方差），MOVER方法通过左右方差分离，能更好的描述参数的分布特征

• 不依赖具体分布假设，仅需输入点估计和置信区间即可计算

---

二、MOVER-R和MOVER-D方法

• MOVER-R（Ratio）用于构建比率参数（R=θ₁/θ₂）的置信区间
• MOVER-D（Difference）用于构建差值参数（D=θ₁-θ₂）的置信区间

流程

输入数据：

输入两样本的：

• θ₁的点估计𝜗̂₁及置信区间 [𝑙̂₁,𝑢̂₁]
• θ₂的点估计𝜗̂₂及置信区间 [𝑙̂₂,𝑢̂₂]
• θ₁与θ₂的相关系数ρ̂

进行方差重估计：

• 计算θ₁的左右方差：σ̂₁₁², σ̂₁₂²
• 计算θ₂的左右方差：σ̂₂₁², σ̂₂₂²

计算分子与分母的左右方差

• 定义点估计 $\hat{\theta}_i$、置信下限 $\hat{l}_i$、置信上限 $\hat{u}_i$。
• 左方差：$\hat{\sigma}_{i1}^2 = \frac{(\hat{\theta}_i - \hat{l}i)^2}{z{\alpha/2}^2}$
• 右方差：$\hat{\sigma}_{i2}^2 = \frac{(\hat{u}_i - \hat{\theta}i)^2}{z{\alpha/2}^2}$​

MOVER-D方法（两参数差值置信区间估计）

目标参数

• 差值型参数：$D = \theta_1 - \theta_2$（率差、均值差）
• 和型参数：$S = \theta_1 + \theta_2$（两指标之和）

左右方差分离

• 方差重估计（基于置信区间信息）：
  $$
  \hat{\sigma}_{i1}^2 = \frac{(\hat{\theta}i - \hat{l}i)^2}{z{\alpha/2}^2}, \quad \hat{\sigma}{i2}^2 = \frac{(\hat{u}_i - \hat{\theta}i)^2}{z{\alpha/2}^2}
  $$

  置信区间的非对称性

  • 当抽样分布偏态时，点估计 $\hat{\theta}_i$ 到置信下限 $\hat{l}i$ 的距离（$\hat{d}{i1}$）与到上限 $\hat{u}i$ 的距离（$\hat{d}{i2}$）不相等

  • 左方差 $\hat{\sigma}_{i1}^2$ 反映 $\theta_i$ 向左偏离的趋势（分布左尾信息）

  • 右方差 $\hat{\sigma}_{i2}^2$ 反映 $\theta_i$ 向右偏离的趋势（分布右尾信息）

    

  1. • 差值置信区间的边界特性

       • 差值$D = \theta_1 - \theta_2$的置信下限 $\hat{L}$ 对应 $\theta_1$ 的最小值和 $\theta_2$ 的最大值组合：
         $$
         \hat{L} \approx \min(\theta_1) - \max(\theta_2) = \hat{l}_1 - \hat{u}_2
         $$

       • 差值$D = \theta_1 - \theta_2$的置信上限 $\hat{U}$ 对应 $\theta_1$ 的最大值和 $\theta_2$ 的最小值组合：
         $$
         \hat{U} \approx \max(\theta_1) - \min(\theta_2) = \hat{u}_1 - \hat{l}_2
         $$

  非对称方差组合：

  • 下限 $\hat{L}$：接近 $\hat{l}1 - \hat{u}2$ → 使用 $\theta_1$ 的左方差（$\hat{\sigma}{11}^2$）和 $\theta_2$ 的右方差（$\hat{\sigma}{22}^2$）。
  • 上限 $\hat{U}$：接近 $\hat{u}1 - \hat{l}2$ → 使用 $\theta_1$ 的右方差（$\hat{\sigma}{12}^2$）和 $\theta_2$ 的左方差（$\hat{\sigma}{21}^2$）。

MOVER-D 置信区间

差值 $D = \theta_1 - \theta_2$ 的置信区间

根据 $\hat{\theta}_i$ 的渐近正态性，$\theta_1 - \theta_2$ 的 Wald 置信区间下限和上限可分别表示为：

$$
\hat{L}{\text{MOVER - D}} = (\hat{\theta}1 - \hat{\theta}2) - z{\alpha/2}\sqrt{\hat{\sigma}{11}^2 - 2\hat{\rho}\hat{\sigma}{11}\hat{\sigma}{22} + \hat{\sigma}{22}^2}
$$
$$
\hat{U}{\text{MOVER - D}} = (\hat{\theta}1 - \hat{\theta}2) + z{\alpha/2}\sqrt{\hat{\sigma}{12}^2 - 2\hat{\rho}\hat{\sigma}{12}\hat{\sigma}{21} + \hat{\sigma}{21}^2}
$$

其中，$\hat{\sigma}_i^2$ 是 $\sigma_i^2$ 的估计。当 $\hat{\theta}_1$ 和 $\hat{\theta}_2$ 相互独立时，$\hat{\rho}$ 取 0。

由于 $\hat{\theta}i$ 分布的不对称性， 当利用 MOVER 法时，可以使用左方差 $\hat{\sigma}{i1}^2$ 或右方差 $\hat{\sigma}_{i2}^2$ 替换式中的 $\hat{\sigma}_i^2$。在求下限 $\hat{L}$ 时，由于 $\hat{L}$ 更为接近 $\hat{l}1 - \hat{u}2$，因而使用 $\hat{\sigma}{11}^2$ 与 $\hat{\sigma}{22}^2$ 分别估计 $\hat{\sigma}_1^2$ 和 $\hat{\sigma}_2^2$ 更为合理；同理， $\hat{U}$ 更为接近 $\hat{u}1 - \hat{l}2$ ，因而可使用 $\hat{\sigma}{12}^2$ 与 $\hat{\sigma}{21}^2$ 分别估计 $\hat{\sigma}_1^2$ 和 $\hat{\sigma}_2^2$。

因此，$\theta_1 - \theta_2$ 的 MOVER-D 置信区间下限和上限可分别表示为：

$$
\hat{L}{\text{MOVER - D}} = (\hat{\theta}1 - \hat{\theta}2) - \sqrt{\hat{d}{11}^2 - 2\hat{\rho}\hat{d}{11}\hat{d}{22} + \hat{d}_{22}^2}
$$

$$
\hat{U}{\text{MOVER - D}} = (\hat{\theta}1 - \hat{\theta}2) + \sqrt{\hat{d}{12}^2 - 2\hat{\rho}\hat{d}{12}\hat{d}{21} + \hat{d}_{21}^2}
$$

$S = \theta_1 + \theta_2$ 的置信区间

与两参数差值的 Wald 置信区间类似，两参数和 $\theta_1 + \theta_2$ 的 Wald 置信区间下限和上限可分别表示为

$$
\hat{L}{\text{MOVER - D}} = (\hat{\theta}1 + \hat{\theta}2) - z{\alpha/2}\sqrt{\hat{\sigma}{11}^2 + 2\hat{\rho}\hat{\sigma}{11}\hat{\sigma}{21} + \hat{\sigma}{21}^2}
$$
$$
\hat{U}{\text{MOVER - D}} = (\hat{\theta}1 + \hat{\theta}2) + z{\alpha/2}\sqrt{\hat{\sigma}{12}^2 + 2\hat{\rho}\hat{\sigma}{12}\hat{\sigma}{22} + \hat{\sigma}{22}^2}
$$

同理，将 $\theta_1 + \theta_2$ 视为 $\theta_1 - (-\theta_2)$，则可将两参数差值的 MOVER-D 置信区间推广至两参数之和的情况，则 $\theta_1 + \theta_2$ 的 MOVER-D 置信区间下限和上限可分别表示为：

$$
\hat{L}{\text{MOVER - D}} = (\hat{\theta}1 + \hat{\theta}2) - \sqrt{\hat{d}{11}^2 + 2\hat{\rho}\hat{d}{11}\hat{d}{21} + \hat{d}{21}^2}
$$
$$
\hat{U}{\text{MOVER - D}} = (\hat{\theta}1 + \hat{\theta}2) + \sqrt{\hat{d}{12}^2 + 2\hat{\rho}\hat{d}{12}\hat{d}{22} + \hat{d}{22}^2}
$$

• $\hat{\theta}_1, \hat{\theta}_2$：分子与分母的点估计
• $\hat{l}_i, \hat{u}_i$：$\hat{\theta}_i$ 的置信区间下限和上限（$\hat{l}_i < \hat{\theta}_i < \hat{u}_i$）
• $\hat{\rho}$：$\hat{\theta}_1$ 与 $\hat{\theta}_2$ 的相关系数估计（独立时为 0）
• $d_{i1}$ 表示点估计值到置信下限的距离（“左方差基础”）
• $d_{i2}$ 表示点估计值到置信上限的距离（“右方差基础”）

MOVER-R：求两参数比R=θ₁/θ₂的置信区间

MOVER-R方法 通过三步构建比值 $R$ 的置信区间：

1. 转化问题：将 $R = \frac{\theta_1}{\theta_2}$ 转化为 $\theta_1 - R\theta_2 = 0$；
2. 分情况构造：按 $R$ 正负选择 MOVER-D $\theta_1 - R\theta_2$ 置信区间形式（式2-5, 2-6）；
3. 反解方程：令置信上下限等于0，求解 $R$ 的上下限（式2-7, 2-8）。
   改进：Zou 等根据分子 $\theta_1$ 置信区间符号动态选择上下限组合。
   局限：依赖分母不跨零

对于 $\theta_1/\theta_2$ 的 MOVER-R 置信区间，Donner 和 Zou[24]提出可以将 $R = \theta_1/\theta_2$ 变换为 $\theta_1 - R\theta_2 = 0$。如果将 $\theta_1 - R\theta_2$ 视为一个差值，则可以使用 MOVER-D 法构造 $\theta_1 - R\theta_2$ 的置信区间，其上下限均为关于 $R$ 的表达式。进一步，由于 $\theta_1 - R\theta_2$ 的真值为 0， 因此 Donner 和 Zou[24]令 $\theta_1 - R\theta_2$ 的 MOVER-D 置信区间上下限都等于 0，求解关于 $R$ 的方程并选取合适的根，则得到 $R$ 的置信区间上下限。MOVER-R 置信区间的计算过程如下：
首先，建立原假设与备择假设：
$$
H_0: \theta_1 - R\theta_2 = 0 \
H_1: \theta_1 - R\theta_2 \neq 0
$$
由于 $\theta_1 - R\theta_2$ 的 MOVER-D 置信区间上下限依赖于 $R$ 的正负，因此：

根据 $R$ 的正负性选择方差组合：

• 当 $R>0$ 时，下限用 $\hat{\sigma}{11}^2$ 和 $\hat{\sigma}{22}^2$，上限用 $\hat{\sigma}{12}^2$ 和 $\hat{\sigma}{21}^2$。
• 当 $R\leq0$ 时，下限用 $\hat{\sigma}{11}^2$ 和 $\hat{\sigma}{21}^2$，上限用 $\hat{\sigma}{12}^2$ 和 $\hat{\sigma}{22}^2$。

当 $R > 0$ 时

对于 $R$ 值为正的情况，$\theta_1 - R\theta_2$ 的下限更接近于 $\hat{l}1 - R\hat{u}2$，上限更接近于 $\hat{u}1 - R\hat{l}2$。将 $\theta_1 - R\theta_2$ 的 MOVER-D 置信区间上下限视为 $R$​ 的函数，则下限和上限可以分别表示为：
$$
\hat{L}{12}® = \hat{\theta}1 - R\hat{\theta}2 - \sqrt{\hat{d}{11}^2 - 2\hat{\rho}\hat{d}{11}\hat{d}{22}R + \hat{d}{22}^2 R^2}
$$
$$
\hat{U}{21}® = \hat{\theta}1 - R\hat{\theta}2 + \sqrt{\hat{d}{12}^2 - 2\hat{\rho}\hat{d}{12}\hat{d}{21}R + \hat{d}{21}^2 R^2}
$$

当 $R \leq 0$ 时

与 $R$ 值为正的情况不同，当 $R$ 值为负时，$\theta_1 - R\theta_2$ 的下限更接近于 $\hat{l}1 - R\hat{l}2$，上限更接近于 $\hat{u}1 - R\hat{u}2$，因此 $\theta_1 - R\theta_2$​ 的 MOVER-D 置信区间的下限和上限可以分别表示为：
$$
\hat{L}{11}® = \hat{\theta}1 - R\hat{\theta}2 - \sqrt{\hat{d}{11}^2 - 2\hat{\rho}\hat{d}{11}\hat{d}{21}R + \hat{d}{21}^2 R^2}
$$
$$
\hat{U}{22}® = \hat{\theta}1 - R\hat{\theta}2 + \sqrt{\hat{d}{12}^2 - 2\hat{\rho}\hat{d}{12}\hat{d}{22}R + \hat{d}{22}^2 R^2}
$$
Donner 和 Zou[24]最初在假设 $R > 0$ 的前提下提出了 MOVER-R 置信区间构造方法，但实际上只有当 $\theta_1$ 的置信区间上下限都为正时，才可以认为 $R > 0$ 是一种合理的假设。由于 $\theta_1 - R\theta_2$ 的 MOVER-D 置信区间有不同的形式，Newcombe[26]指出，当 $\theta_1$ 置信区间的上限或下限为负时 Donner 和 Zou[24]的方法有误，并提出了在 $R < 0$ 时的置信区间上下限形式。在此基础上，Zou 等[27]进一步发展了考虑分子置信区间上下限正负性的 MOVER-R 法。

当 $R > 0$ 时

分别限制 $\theta_1 - R\theta_2$ 的 MOVER-D 置信区间的下限等于 0 和上限等于 0，即令 $\hat{L}{12}® = 0$ 和 $\hat{U}{21}® = 0$ ， 取方程 $\hat{L}{12}® = 0$ 的两个根中较小的那个作为 $R$ 的 MOVER-R 置信区间的下限，取方程 $\hat{U}{21}® = 0$ 两个根中较大的那个作为 $R$ 的 MOVER-R 置信区间的上限，分别表示如下：
$$
\hat{R}_{L+} = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{22} - \sqrt{[\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{22}]^2 - \hat{l}_1\hat{u}_2(2\hat{\theta}_1 - \hat{l}_1)(2\hat{\theta}_2 - \hat{u}_2)}}{\hat{u}_2(2\hat{\theta}_2 - \hat{u}2)}
$$
$$
\hat{R}{U+} = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{12}\hat{d}{21} + \sqrt{[\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{12}\hat{d}{21}]^2 - \hat{u}_1\hat{l}_2(2\hat{\theta}_1 - \hat{u}_1)(2\hat{\theta}_2 - \hat{l}_2)}}{\hat{l}_2(2\hat{\theta}_2 - \hat{l}_2)}
$$

• $\hat{\theta}_1, \hat{\theta}_2$：分子与分母的点估计
• $\hat{l}_i, \hat{u}_i$：$\hat{\theta}_i$ 的置信区间下限和上限（$\hat{l}_i < \hat{\theta}_i < \hat{u}_i$）
• $\hat{\rho}$：$\hat{\theta}_1$ 与 $\hat{\theta}_2$ 的相关系数估计（独立时为 0）
• $d_{i1}$ 表示点估计值到置信下限的距离（“左方差基础”）
• $d_{i2}$ 表示点估计值到置信上限的距离（“右方差基础”）

当 $R \leq 0$ 时

令 $\hat{L}{11}® = 0$ 和 $\hat{U}{22}® = 0$​，类似地分别取相应的根作为 MOVER-R 置信区间下限和上限，分别表示如下：
$$
\hat{R}_{L-} = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{21} - \sqrt{[\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{21}]^2 - \hat{l}_1\hat{l}_2(2\hat{\theta}_1 - \hat{l}_1)(2\hat{\theta}_2 - \hat{l}_2)}}{\hat{l}_2(2\hat{\theta}_2 - \hat{l}2)}
$$
$$
\hat{R}{U-} = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{12}\hat{d}{22} + \sqrt{[\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{12}\hat{d}{22}]^2 - \hat{u}_1\hat{u}_2(2\hat{\theta}_1 - \hat{u}_1)(2\hat{\theta}_2 - \hat{u}_2)}}{\hat{l}_2(2\hat{\theta}_2 - \hat{u}_2)}
$$

• $\hat{\theta}_1, \hat{\theta}_2$：分子与分母的点估计
• $\hat{l}_i, \hat{u}_i$：$\hat{\theta}_i$ 的置信区间下限和上限（$\hat{l}_i < \hat{\theta}_i < \hat{u}_i$）
• $\hat{\rho}$：$\hat{\theta}_1$ 与 $\hat{\theta}_2$ 的相关系数估计（独立时为 0）
• $d_{i1}$ 表示点估计值到置信下限的距离（“左方差基础”）
• $d_{i2}$ 表示点估计值到置信上限的距离（“右方差基础”）

Newcombe[26]和 Zou 等[27]在推导过程中假设分母 $\theta_2$ 的置信区间的上下限均大于 0。此时，应根据分子置信区间的上下限符号来选择 $R$ 的置信区间上下限，MOVER - R 置信区间可以表示为：
（1）当 $0 < \hat{l}1 < \hat{u}1$ 时，$(\hat{R}{L+}, \hat{R}{U+})$
（2）当 $\hat{l}1 \leq 0 < \hat{u}1$ 时，$(\hat{R}{L-}, \hat{R}{U+})$
（3）当 $\hat{l}1 < \hat{u}1 \leq 0$ 时，$(\hat{R}{L-}, \hat{R}{U-})$

特别地，当 $\hat{u}2 = 2\hat{\theta}2$ 时，$\hat{R}{L+}$ 和 $\hat{R}{U-}$ 分别替换为
$$
\hat{R}_{L+} = \frac{\hat{l}_1(2\hat{\theta}_1 - \hat{l}_1)}{2\hat{\theta}_1\hat{\theta}_2 - \hat{\rho}(\hat{\theta}_1 - \hat{l}_1)\hat{\theta}2}
$$
$$
\hat{R}{U-} = \frac{\hat{u}_1(2\hat{\theta}_1 - \hat{u}_1)}{\hat{\theta}_1\hat{\theta}_2 - 2\hat{\rho}(\hat{u}_1 - \hat{\theta}_1)\hat{\theta}_2}
$$

存在的问题：

尽管通过引入分子和分母的非对称置信区间，MOVER - R 法可以很好地考虑分子和分母抽样分布的偏态性，然而目前的 MOVER - R 法依赖于分母的置信区间不包含 0 这一条件，即需要假设分母 $\theta_2$ 的置信区间上下限均大于 0。如果分母的置信区间包含 0，那么比值有可能取到 $-\infty$ 或 $+\infty$；另外，$R$​ 的置信区间上下限根号下的部分也可能取到负数。对于根号下部分可能为负的情况，Donner 和 Zou[24]在构造变异系数的置信区间时，将根号下的部分替换为 0。但其模拟研究显示，当分母拒绝为 0 的检验效能较低时，其置信区间的覆盖率会严重低于名义水平。

综上所述，有必要将分母的置信区间包含 0 的这一情况考虑在内，将 MOVER - R 法扩展至整个参数空间。因此，本研究提出了将 MOVER - R 法扩展至整个参数空间的 EMOVER - R 法，见 2.2 节。

EMOVER-R法

EMOVER-R法（Extended MOVER-R）是 MOVER-R 的扩展版本，由本研究作者提出，专门解决分母置信区间包含0时传统 MOVER-R 失效的问题

EMOVER-R 的提出背景

MOVER-R 的核心缺陷

• 前提限制：传统 MOVER-R 要求分母 $\theta_2$ 的置信区间严格不跨零（即 $l_2 > 0$ 或 $u_2 < 0$）。

• 实际问题：当 $\theta_2$ 的置信区间包含 0（如 $[-0.2, 0.3]$）：

  1. 比值 $R = \frac{\theta_1}{\theta_2}$ 可能趋于 $\pm\infty$，导致置信区间无界。
  2. 置信区间根号内项 $\Delta$ 可能为负，需强制设为 0（如 Donner & Zou 的做法），导致覆盖率显著低于名义水平（如 95%）。

EMOVER-R 的核心创新

在不依赖 $\theta_2$ 是否跨零的前提下，直接构造 $R$ 的置信区间：

1. 重新定义方差估计：
   扩展传统左右方差形式，允许分母置信区间包含 0。
2. 引入连续性修正项：
   通过引入调节项 $\delta$ 解决根号内为负的问题。
3. 理论证明一致性：
   在分母接近 0 时仍保持大样本性质（原文 2.2 节）。

---

流程：

1.参数定义

输入两样本的：

• θ₁的点估计𝜗̂₁及置信区间 [𝑙̂₁,𝑢̂₁]
• θ₂的点估计𝜗̂₂及置信区间 [𝑙̂₂,𝑢̂₂]
• θ₁与θ₂的相关系数ρ̂

进行方差重估计：

• 计算θ₁的左右方差：σ̂₁₁², σ̂₁₂²
• 计算θ₂的左右方差：σ̂₂₁², σ̂₂₂²

计算分子与分母的左右方差

• 定义点估计 $\hat{\theta}_i$、置信下限 $\hat{l}_i$、置信上限 $\hat{u}_i$。
• 左方差：$\hat{\sigma}_{i1}^2 = \frac{(\hat{\theta}_i - \hat{l}i)^2}{z{\alpha/2}^2}$
• 右方差：$\hat{\sigma}_{i2}^2 = \frac{(\hat{u}_i - \hat{\theta}i)^2}{z{\alpha/2}^2}$

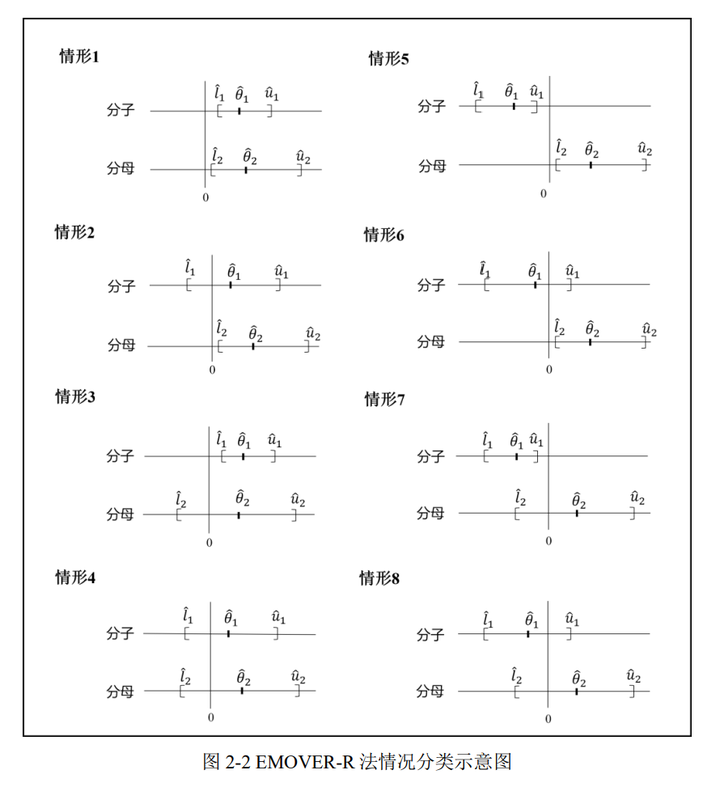
2.分类八个情形及其处理办法

EMOVER-R 方法将 分子（$\theta_1$） 和 分母（$\theta_2$） 的置信区间相对于 零点（0） 的位置关系分为 8 种情形。分类依据：

• 分子/分母的位置：区间完全在 0 左侧（负值）、完全在右侧（正值）、或跨过 0。
• 点估计 $\hat{\theta}_i$ 的位置：靠近置信下限（$\hat{l}_i$）或上限（$\hat{u}_i$）。

---

八个情形及其处理办法

情形	分子 ($\theta_1$) 区间位置	分母 ($\theta_2$) 区间位置	处理办法
情形1	完全在 0 右侧 （$\hat{l}_1>0$）	完全在 0 右侧 （$\hat{l}_2>0$）	使用标准 MOVER-R 的 $R>0$ 公式（式 2-7）	两参数均为正（如风险比 RR > 0）
情形2	完全在 0 右侧 （$\hat{l}_1>0$）	跨过 0 （$\hat{l}_2<0<\hat{u}_2$）	引入调节项 $\delta$，避免分母接近 0 时区间失真	分母微弱效应（如药物副作用率接近 0）
情形3	完全在 0 右侧 （$\hat{l}_1>0$）	完全在 0 左侧 （$\hat{u}_2<0$）	分子分母同乘 −1 后转为情形 1	分母为负（如成本节省比例）
情形4	跨过 0 （$\hat{l}_1<0<\hat{u}_1$）	完全在 0 右侧 （$\hat{l}_2>0$）	结合 $\theta_1$ 实际值选 $R\leq0$ 或 $R>0$ 公式	分子有正负波动（如净收益比）
情形5	跨过 0 （$\hat{l}_1<0<\hat{u}_1$）	跨过 0 （$\hat{l}_2<0<\hat{u}_2$）	使用 EMOVER-R 的 $\delta$ 修正公式	分子分母均微弱（如生态学弱效应比）
情形6	跨过 0 （$\hat{l}_1<0<\hat{u}_1$）	完全在 0 左侧 （$\hat{u}_2<0$）	分子分母同乘 −1 后转为情形 4	分母为负且分子跨零
情形7	完全在 0 左侧 （$\hat{u}_1<0$）	完全在 0 右侧 （$\hat{l}_2>0$）	使用 $R\leq0$ 公式（式 2-8）	分子为负、分母为正（如亏损率）
情形8	完全在 0 左侧 （$\hat{u}_1<0$）	跨过 0 （$\hat{l}_2<0<\hat{u}_2$）	同情形 2：引入 $\delta$ 调节分母接近 0 的影响	分子负向、分母微弱效应

---

分母跨零（情形 2,5,8）

1. 情形2：
   • 分子：完全在0右侧（$\hat{l}_1>0$）
   • 分母：区间跨过0点（$\hat{l}_2<0<\hat{u}_2$）
   • 图示：分母水平线从左下（负）延伸至右上（正），分子水平线全程在正区域。
2. 情形5：
   • 分子：区间跨过0点（$\hat{l}_1<0<\hat{u}_1$）
   • 分母：区间跨过0点（$\hat{l}_2<0<\hat{u}_2$）
   • 图示：分子分母的水平线均跨越0轴，形成十字交叉状。
3. 情形8：
   • 分子：完全在0左侧（$\hat{u}_1<0$）
   • 分母：区间跨过0点（$\hat{l}_2<0<\hat{u}_2$）
   • 图示：分子水平线全程在负区域，分母水平线跨越0轴。

共同点：分母置信区间包含0（$\hat{l}_2<0<\hat{u}_2$），即 $\theta_2$ 可能为正、负或零。

步骤1：引入调节项 $\delta$

• 目的：解决根号项 $\Delta < 0$ 问题
• 定义：$\delta = O_p(n^{-1})$
• 计算规则：
  $$
  \delta = n^k \cdot \hat{\theta}_2
  $$
  其中 $k = 0.5 \sim 1$（经验常数），$n$ 为样本量
• 性质：$\delta \to 0$ 当 $n \to \infty$

步骤2：改进置信区间计算

通用修正公式：
$$
\hat{R}_L = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{22} - \sqrt{\Delta + \delta}}{\hat{u}_2(2\hat{\theta}_2 - \hat{u}_2)}, \quad \hat{R}_U = \frac{\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{12}\hat{d}{21} + \sqrt{\Delta + \delta}}{\hat{l}_2(2\hat{\theta}_2 - \hat{l}_2)}
$$
其中：
$$
\Delta = [\hat{\theta}1\hat{\theta}2 - \hat{\rho}\hat{d}{11}\hat{d}{22}]^2 - \hat{l}_1\hat{u}_2(2\hat{\theta}_1 - \hat{l}_1)(2\hat{\theta}_2 - \hat{u}_2)
$$

分子跨零（情形 4,5,6）

• 根据 $\theta_1$ 实际值的正负选择公式：
  • 若 $\theta_1 > 0 \to$ 按 $R > 0$ 处理
  • 若 $\theta_1 \leq 0 \to$ 按 $R \leq 0$ 处理

1. 同乘 −1 转换（情形 3,6）：
   • 原理：$R = \frac{\theta_1}{\theta_2} = \frac{-\theta_1}{-\theta_2}$。
   • 操作：将 $\theta_1’ = -\theta_1, \theta_2’ = -\theta_2$ 后转为标准情形（如情形 1 或 4）。

---

四、解决的核心问题

1. 分母置信区间包含 0 时的处理

假设 $\theta_2$ 的 95% CI 为 $[-0.1, 0.2]$：

• 传统 MOVER-R：根号内 $\Delta < 0$ → 需手动设 $\Delta = 0$ → 置信区间失真（覆盖率降至 85%）。
• EMOVER-R：通过 $\delta > 0$ 确保 $\Delta + \delta$ 有效，且 $\delta$ 随样本量增加趋于 0 → 覆盖率稳定接近 95%。

2. 泰勒展开证明

原文通过一阶泰勒展开证明：
$$
\sqrt{\Delta + \delta} - \sqrt{\Delta} = O_p(n^{-1/2})
$$
当 $n \to \infty$ 时，即使 $\theta_2 \to 0$，EMOVER-R 的置信区间仍保持渐近精确覆盖。