数据结构-树

First Post:

2025-04-30

Last Update:

2025-09-30

Page View: loading...

树是常用的数据结构之一，种类很多比如二叉树，二叉查找树，平衡二叉树，红黑树，B 树，B+树等，本身就是一种递归结构

什么是树？

树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家谱、单位的组织架构、等等。

在计算机科学中，树是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

每个节点都只有有限个子节点或无子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树；
树里面没有环路(cycle)

术语

节点的度：一个节点含有的子树的个数称为该节点的度；
树的度：一棵树中，最大的节点度称为树的度；
叶节点或终端节点：度为零的节点；
非终端节点或分支节点：度不为零的节点；
父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
兄弟节点：具有相同父节点的节点互称为兄弟节点；
节点的层次：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推；
深度：对于任意节点 n,n 的深度为从根到 n 的唯一路径长，根的深度为 0；
高度：对于任意节点 n,n 的高度为从 n 到一片树叶的最长路径长，所有树叶的高度为 0；
堂兄弟节点：父节点在同一层的节点互为堂兄弟；
节点的祖先：从根到该节点所经分支上的所有节点；
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
森林：由 m（m>=0）棵互不相交的树的集合称为森林；

                    A (根节点)
                   / \
                  B   C
                 / \   \
                D   E   F
               /       / \
              G       H   I (叶节点)
             / \
            J   K (叶节点)


- A是根节点，没有父节点
- B是A的子节点，A是B的父节点
- B和C是兄弟节点（具有相同父节点A）
- G是叶节点（度为0）
- B是非终端节点（度不为0，度为2）
- 从A到K的路径长度为3，K的深度为3
- 树的度为2（B节点的度最大）
- B的度为2（有两个子节点D和E）
- 整个结构是一个有序树（子节点有左右顺序）

这个图示展示了以下树的基本概念：

根节点：A 节点，整棵树的起始点
父节点与子节点关系：如 A 是 B 和 C 的父节点，B 和 C 是 A 的子节点
兄弟节点：B 和 C 具有相同的父节点 A，所以它们是兄弟节点
叶节点：G、H、I、J、K 这些没有子节点的节点
内部节点：A、B、C、D、E、F 这些有子节点的节点
节点的度：B 的度为 2（有两个子节点），G 的度为 2（有两个子节点）
树的度：整棵树的最大节点度，这里是 2
路径与深度：从根节点 A 到任意节点的路径，如 A->B->D->G 的路径长度为 3

树的种类

有序/无序：

无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。
有序树/搜索树/查找树：树中任意节点的子节点之间有顺序关系，这种树称为有序树。即树的所有节点按照一定的顺序排列，这样进行插入、删除、查找时效率就会非常高

平衡/不平衡：

平衡树
- 绝对平衡树：所有叶节点在同一层
- 非绝对平衡树
不平衡树

节点的分叉情况：

等叉树：是每个节点的键值个数都相同、子节点个数也都相同
- 二叉树：每个节点最多含有两个子树的树称为二叉树；
  - 完全二叉树：除了第 d 层外，其它各层的节点数目均已达最大值，且第 d 层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树；
    - 满二叉树：所有叶节点都在最底层的完全二叉树；
  - 平衡二叉树、AVL 树：当且仅当任何节点的两棵子树的高度差不大于 1 的二叉树；
  - 排序二叉树：也称二叉查找树、二叉搜索树、有序二叉树；
- 霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
- 多叉树
不等叉树：每个节点的键值个数不一定相同、子节点个数也不一定相同
- B 树：对不等叉树的节点键值数和插入、删除逻辑添加一些特殊的要求，使其能达到绝对平衡的效果。B 树全称 Balance Tree。如果某个 B 树上所有节点的分叉数最大值是 m，则把这个 B 数叫做 m 阶 B 树。

二叉树

二叉树就像它的名字一样，每个元素最多有两个节点，分别称为左节点和右节点。当然并不是每个元素都需要有两个节点，有的可能只有左节点，有的可能只有右节点。

        A (根节点)
       / \
      B   C
     / \   \
    D   E   F
   /       / \
  G       H   I (叶节点)
 / \
J   K (叶节点)

基于树的存储模式的不同，为了更好的利用存储空间，二叉树又分为完全二叉树和非完全二叉树：

「完全二叉树」：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大

１、完全二叉树

                    A (根节点)
                   / \
                  B   C
                 / \   \
                D   E   F
               /       / \
              G       H   I (叶节点)
             / \
            J   K (叶节点)

完全二叉树的顺序存储
数组索引: [0][1][2][3][4][5][6][7][8]
存储内容: [1][2][3][4][5][6][7][8][9]

２、非完全二叉树

        1
       / \
      2   3
     /     \
    4       5
   /       / \
  6       7   8
         /
        9

非完全二叉树的顺序存储
数组索引: [0][1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18]
存储内容: [1][2][3][4][ ][ ][5][6][ ][ ][ ][ ][ ][7][8][ ][ ][ ][9]
存在大量空位，造成空间浪费

二叉树的存储模式

二叉树的存储模式有两种，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法

二叉链式存储法

链式存储法相对比较简单，理解起来也非常容易，每一个节点都有三个字段，一个字段存储着该节点的值，另外两个字段存储着左右节点的引用。我们顺着跟字节就可以很轻松的把整棵树串起来

链式存储法结构示意图：

    节点A
   /     \
  ↓       ↓
节点B    节点C
/   \     /   \
↓    ↓   ↓    ↓
...  ... ...  ...

每个节点的内存结构：
┌─────────────┬─────────────┬─────────────┐
│    data     │    left     │    right    │
│  (节点值)   │  (左子节点) │  (右子节点) │
└─────────────┴─────────────┴─────────────┘
      ↓              ↓             ↓
    节点值       指向左子树    指向右子树
                   的指针        的指针

链式存储法的 C 语言实现：

#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct TreeNode {
    int data;           // 节点数据
    struct TreeNode* left;   // 左子节点指针
    struct TreeNode* right;  // 右子节点指针
} TreeNode;

// 创建新节点
TreeNode* createNode(int data) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 示例：构建一个简单的二叉树
TreeNode* buildSampleTree() {
    TreeNode* root = createNode(1);
    root->left = createNode(2);
    root->right = createNode(3);
    root->left->left = createNode(4);
    root->left->right = createNode(5);
    return root;
}

// 释放链式存储的二叉树内存
void freeTree(TreeNode* root) {
    if (root == NULL) {
        return;
    }
    freeTree(root->left);
    freeTree(root->right);
    free(root);
}

// 使用示例
void demonstrateStorageMethods() {
    printf("=== 二叉树两种存储方式演示 ===\n");

    // 1. 链式存储法
    printf("\n1. 链式存储法:\n");
    TreeNode* linkedTree = buildSampleTree();
    printf("前序遍历结果: ");
    preOrderLinked(linkedTree);
    printf("\n");
    freeTree(linkedTree);

    // 2. 顺序存储法
    printf("\n2. 顺序存储法:\n");
    buildCompleteBinaryTree();
    printArrayTree();
    printf("前序遍历结果: ");
    preOrderArray(0);
    printf("\n");
}

/*
对比两种存储方式：

1. 链式存储法：
   - 优点：灵活，不需要大片连续内存，插入删除节点方便
   - 缺点：需要额外空间存储指针，遍历时需要多次内存跳转

2. 顺序存储法：
   - 优点：节省指针空间，访问节点速度快（通过数组下标直接访问）
   - 缺点：对于非完全二叉树会造成空间浪费，插入删除节点复杂
*/

int main() {
    demonstrateStorageMethods();
    return 0;
}

顺序存储法

顺序存储法是基于数组实现的，数组是一段有序的内存空间，如果我们把跟节点的坐标定位i=1，左节点就是 2 i = 2，右节点 2 i+ 1 = 3，以此类推，每个节点都这么算，然后就将树转化成数组了，反过来，按照这种规则我们也能将数组转化成一棵树。

于是在这里我们就能发现一个问题：如果这是一颗不平衡的二叉树是不是会造成大量的空间浪费？这就是为什么需要分完全二叉树和非完全二叉树，分别来看看这两种树基于数组的存储模式。

顺序存储法的 C 语言实现：

#include <stdio.h>
#include <stdlib.h>
#define MAX_TREE_SIZE 100

// 用数组表示二叉树
int treeArray[MAX_TREE_SIZE];
int treeSize = 0;

// 初始化数组
void initTreeArray() {
    for (int i = 0; i < MAX_TREE_SIZE; i++) {
        treeArray[i] = -1; // -1表示空节点
    }
}

// 在指定位置插入节点
void insertNode(int index, int data) {
    if (index >= MAX_TREE_SIZE) {
        printf("数组越界\n");
        return;
    }
    treeArray[index] = data;
    if (index >= treeSize) {
        treeSize = index + 1;
    }
}

// 获取父节点索引
int getParentIndex(int index) {
    if (index <= 0) return -1;
    return (index - 1) / 2;
}

// 获取左子节点索引
int getLeftChildIndex(int index) {
    int leftIndex = 2 * index + 1;
    return (leftIndex < MAX_TREE_SIZE) ? leftIndex : -1;
}

// 获取右子节点索引
int getRightChildIndex(int index) {
    int rightIndex = 2 * index + 2;
    return (rightIndex < MAX_TREE_SIZE) ? rightIndex : -1;
}

// 示例：构建完全二叉树
void buildCompleteBinaryTree() {
    initTreeArray();
    // 构建一个简单的完全二叉树: 1, 2, 3, 4, 5
    //       1
    //      / \
    //     2   3
    //    / \
    //   4   5
    insertNode(0, 1);  // 根节点
    insertNode(1, 2);  // 1的左子节点
    insertNode(2, 3);  // 1的右子节点
    insertNode(3, 4);  // 2的左子节点
    insertNode(4, 5);  // 2的右子节点
}

// 打印数组表示的二叉树（层序遍历）
void printArrayTree() {
    printf("数组存储的二叉树: ");
    for (int i = 0; i < treeSize; i++) {
        if (treeArray[i] != -1) {
            printf("%d ", treeArray[i]);
        } else {
            printf("NULL ");
        }
    }
    printf("\n");
}

// 前序遍历（数组实现）
void preOrderArray(int index) {
    if (index >= treeSize || treeArray[index] == -1) {
        return;
    }
    printf("%d ", treeArray[index]);
    preOrderArray(2 * index + 1);  // 左子树
    preOrderArray(2 * index + 2);  // 右子树
}

// 前序遍历（链式存储）
void preOrderLinked(TreeNode* root) {
    if (root == NULL) {
        return;
    }
    printf("%d ", root->data);
    preOrderLinked(root->left);
    preOrderLinked(root->right);
}

对比两种存储方式：

链式存储法：
- 优点：灵活，不需要大片连续内存，插入删除节点方便
- 缺点：需要额外空间存储指针，遍历时需要多次内存跳转
顺序存储法：
- 优点：节省指针空间，访问节点速度快（通过数组下标直接访问）
- 缺点：对于非完全二叉树会造成空间浪费，插入删除节点复杂

完全二叉树顺序存储法

完全二叉树结构：
        1
       / \
      2   3
     / \ / \
    4  5 6  7
   /
  8

数组存储方式（索引从0开始）：
索引:  [0][1][2][3][4][5][6][7]
值:    [1][2][3][4][5][6][7][8]

父子节点关系：
- 父节点索引为 i，则左子节点索引为 2*i+1，右子节点索引为 2*i+2
- 子节点索引为 j，则父节点索引为 (j-1)/2（整数除法）

具体对应关系：
- 节点1(索引0): 左子节点2(索引1), 右子节点3(索引2)
- 节点2(索引1): 左子节点4(索引3), 右子节点5(索引4)
- 节点3(索引2): 左子节点6(索引5), 右子节点7(索引6)
- 节点4(索引3): 左子节点8(索引7), 无右子节点
- 节点5-8(索引4-7): 均为叶节点，无子节点

非完全二叉树顺序存储法

完全二叉树结构：
        1
       / \
      2   3
     / \ / \
    4  5 6  7
   /
  8

数组存储方式（索引从0开始）：
索引:  [0][1][2][3][4][5][6][7]
值:    [1][2][3][4][5][6][7][8]

父子节点关系：
- 父节点索引为 i，则左子节点索引为 2*i+1，右子节点索引为 2*i+2
- 子节点索引为 j，则父节点索引为 (j-1)/2（整数除法）

具体对应关系：
- 节点1(索引0): 左子节点2(索引1), 右子节点3(索引2)
- 节点2(索引1): 左子节点4(索引3), 右子节点5(索引4)
- 节点3(索引2): 左子节点6(索引5), 右子节点7(索引6)
- 节点4(索引3): 左子节点8(索引7), 无右子节点
- 节点5-8(索引4-7): 均为叶节点，无子节点

从图中将树转化成数组之后可以看出，完全二叉树用数组来存储只浪费了一个下标为 0 的存储空间，非完全二叉树则浪费了大量的空间。
「如果树为完全二叉树，用数组存储比链式存储节约空间，因为数组存储不需要存储左右节点的信息」

二叉树遍历

要了解二叉树的遍历，我们首先需要实例化出一颗二叉树，我们采用链式存储的方式来定义树，实例化树需要树的节点信息，用来存放该节点的信息，因为我们才用的是链式存储，所以我们的节点信息如下。

/**
 * 定义一棵树
 */
/* 树节点的定义 */
#define MAX_TREE_SIZE 100

typedef struct
{
  TElemType data;
  int parent; /* 父节点位置域 */
} PTNode;

typedef struct
{
  PTNode nodes[MAX_TREE_SIZE];
  int n; /* 节点数 */
} PTree;

/* 二叉树节点的定义 */
typedef struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
} TreeNode;

使用 PTNode 结构体表示树的节点，包含：
- data：存储节点数据（类型为 TElemType）
- parent：存储父节点在数组中的索引位置
使用 PTree 结构体表示整棵树，包含：
- nodes：节点数组，最多可容纳 MAX_TREE_SIZE 个节点
- n：实际节点数量

定义完节点信息之后，我们就可以初始化一颗树啦，下面是初始化树的过程:

TreeNode* buildTree() {
// 创建测试用的二叉树
TreeNode* t1 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t2 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t3 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t4 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t5 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t6 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t7 = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* t8 = (TreeNode\*)malloc(sizeof(TreeNode));

    t1->data = 1;
    t2->data = 2;
    t3->data = 3;
    t4->data = 4;
    t5->data = 5;
    t6->data = 6;
    t7->data = 7;
    t8->data = 8;

    t1->left = t2;
    t1->right = t3;
    t2->left = t4;
    t4->right = t7;
    t3->left = t5;
    t3->right = t6;
    t6->left = t8;

    t2->right = NULL;
    t3->left = t5;
    t3->right = t6;
    t4->left = NULL;
    t4->right = t7;
    t5->left = NULL;
    t5->right = NULL;
    t6->left = t8;
    t6->right = NULL;
    t7->left = NULL;
    t7->right = NULL;
    t8->left = NULL;
    t8->right = NULL;

    return t1;

}

经过上面步骤之后，我们的树就长成下图所示的样子，数字代表该节点的值。

构建的二叉树结构：

        1
       / \
      2   3
     /   / \
    4   5   6
     \     /
      7   8

t1->left = t2; // 节点1的左子节点是节点2
t1->right = t3; // 节点1的右子节点是节点3
t2->left = t4; // 节点2的左子节点是节点4
t4->right = t7; // 节点4的右子节点是节点7
t3->left = t5; // 节点3的左子节点是节点5
t3->right = t6; // 节点3的右子节点是节点6
t6->left = t8; // 节点6的左子节点是节点8

节点连接关系：
- 节点1是根节点，左子节点为2，右子节点为3
- 节点2的左子节点为4，右子节点为NULL
- 节点3的左子节点为5，右子节点为6
- 节点4的左子节点为NULL，右子节点为7
- 节点5的左子节点为NULL，右子节点为NULL
- 节点6的左子节点为8，右子节点为NULL
- 节点7和8都是叶节点，没有子节点

有了树之后，我们就可以对树进行遍历
二叉树的遍历有三种方式，前序遍历，中序遍历，后续遍历三种遍历方式，三种遍历方式与节点输出的顺序有关系

前序遍历

「前序遍历」：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。

动图封面

理解了前序遍历的概念和看完前序遍历执行流程动态图之后，你心里一定很想知道，在代码中如何怎么实现树的前序遍历？二叉树的遍历非常简单，一般都是采用递归的方式进行遍历，我们来看看前序遍历的代码：


// 先序遍历，递归实现 先打印本身，再打印左节点，在打印右节点
void preOrder(TreeNode\* root) {
if (root == NULL) {
return;
}
// 输出本身
printf("%d ", root->data);
// 遍历左节点
preOrder(root->left);
// 遍历右节点
preOrder(root->right);
}

中序遍历

「中序遍历」：对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。

跟前序遍历一样，我们来看看中序遍历的执行流程动态图。

动图封面

中序遍历的代码：


// 中序遍历 先打印左节点，再输出本身，最后输出右节点
void inOrder(TreeNode\* root) {
if (root == NULL) {
return;
}
inOrder(root->left);
printf("%d ", root->data);
inOrder(root->right);
}

后序遍历

「后序遍历」：对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

跟前两种遍历一样，理解概念之后，我们还是先来看张图。

动图封面

后序遍历的实现代码：


// 后序遍历 先打印左节点，再输出右节点，最后才输出本身
void postOrder(TreeNode\* root) {
if (root == NULL) {
return;
}
postOrder(root->left);
postOrder(root->right);
printf("%d ", root->data);
}

二叉树有三种遍历方式，但都是一样的，只是输出的顺序不一样

接下来还有一种常用而且比较特殊的二叉树：「二叉查找树」

二叉查找树

二叉查找树又叫二叉搜索树，从名字中我们就能够知道，这种树在查找方面一定有过人的优势，事实确实如此，二叉查找树确实是为查找而生的树，但是它不仅仅支持快速查找数据，还支持快速插入、删除一个数据

「二叉查找树」：在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值，下面定义了一颗二叉查找树

        62
       /  \
      58   88
     /  \ /  \
    47  51 73  99
   /           /
  35          93
   \
    37
   /  \
  36  39
       \
        42

- 对于任意节点，其左子树中的所有节点值都小于该节点值
- 其右子树中的所有节点值都大于该节点值
- 根节点 `62`：左子树所有节点（58, 47, 35, 37, 36, 39, 42, 51）都小于 62；右子树所有节点（88, 73, 99, 93）都大于 62
- 节点 `58`：左子树（47, 35, 37, 36, 39, 42）都小于 58；右子树（51）大于 58
- 节点 `88`：左子树（73）小于 88；右子树（99, 93）大于 88

根据二叉查找树的定义，每棵树的左节点的值要小于这父节点，右节点的值要大于父节点
下面从二叉查找树的查找开始学习二叉查找树

二叉查找树的查找操作

由于二叉查找树的特性，我们需要查找一个数据，先跟跟节点比较，如果值等于跟节点，则返回根节点，如果小于根节点，则必然在左子树这边，只要递归查找左子树就行，如果大于，这在右子树这边，递归右子树即可。这样就能够实现快速查找，因为每次查找都减少了一半的数据，跟二分查找有点相似，快速插入、删除都是居于这个特性实现的。

下面用一幅动态图来加强对二叉查找树查找流程的理解，在上面的这颗二叉查找树中找出值等于 37 的节点：

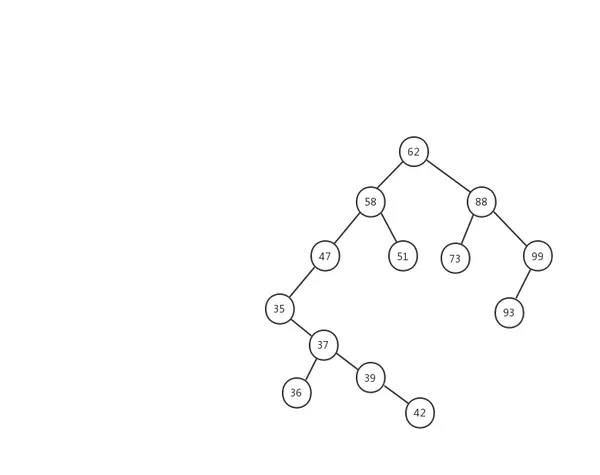
1、先用 37 跟 62 比较，37 < 62 ，在左子树中继续查找
２、左子树的节点值为 58，37 < 58 ，继续在左子树中查找
３、左子树的节点值为 47，37 < 47，继续在左子树中查找
４、左子树的节点值为 35，37 > 35，在右子树中查找
５、右子树中的节点值为 37，37 = 37 ，返回该节点

讲完了查找的概念之后，我们一起来看看二叉查找树的查找操作的代码实现


/**
 * 在二叉查找树中查找指定值的节点
 * @param tree 二叉查找树的根节点
 * @param data 要查找的数据值
 * @return 找到的节点指针，如果未找到则返回NULL
 */
TreeNode* find(TreeNode* tree, int data) {
    // 从根节点开始遍历
    TreeNode* current = tree;

    // 当当前节点不为空时继续查找
    while (current != NULL) {
        // 如果要查找的值小于当前节点值，在左子树中查找
        if (data < current->data) {
            current = current->left;
        }
        // 如果要查找的值大于当前节点值，在右子树中查找
        else if (data > current->data) {
            current = current->right;
        }
        // 如果值相等，找到了目标节点
        else {
            return current;
        }
    }

    // 未找到目标节点
    return NULL;
}

二叉查找树的插入操作

插入跟查找差不多，也是从根节点开始找，如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置。同理，如果要插入的数据比节点数值小，并且节点的左子树为空，就将新数据插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置。

假设我们要插入 63 ，我们用一张动态图来看看插入的流程。

动图封面

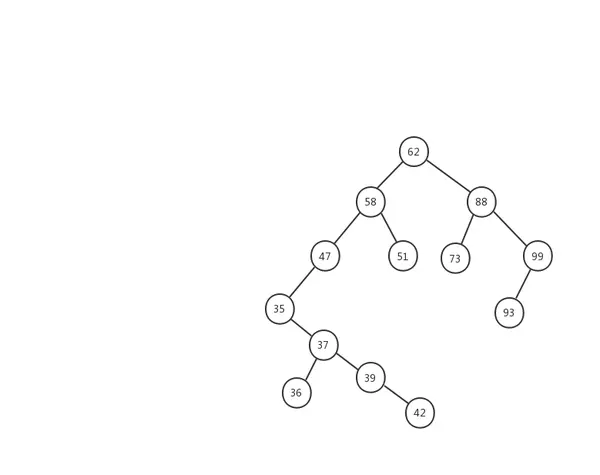
1、63 > 62 ，在树的右子树继续查找.
2、63 < 88 ，在树的左子树继续查找
3、63 < 73 ,因为 73 是叶子节点，所以 63 就成为了 73 的左子树。

我们来看看二叉查找树的插入操作实现代码

/**
 * 在二叉查找树中查找指定值的节点
 * @param tree 二叉查找树的根节点
 * @param data 要查找的数据值
 * @return 找到的节点指针，如果未找到则返回NULL
 */
TreeNode* find(TreeNode* tree, int data) {
    // 从根节点开始遍历
    TreeNode* current = tree;

    // 当当前节点不为空时继续查找
    while (current != NULL) {
        // 如果要查找的值小于当前节点值，在左子树中查找
        if (data < current->data) {
            current = current->left;
        }
        // 如果要查找的值大于当前节点值，在右子树中查找
        else if (data > current->data) {
            current = current->right;
        }
        // 如果值相等，找到了目标节点
        else {
            return current;
        }
    }

    // 未找到目标节点
    return NULL;
}

二叉查找树的删除操作

删除的逻辑要比查找和插入复杂一些，删除分一下三种情况：

「第一种情况」：如果要删除的节点没有子节点，我们只需要直接将父节点中，指向要删除节点的指针置为 null。比如图中的删除节点 51。

「第二种情况」：如果要删除的节点只有一个子节点（只有左子节点或者右子节点），我们只需要更新父节点中，指向要删除节点的指针，让它指向要删除节点的子节点就可以了。比如图中的删除节点 35。

「第三种情况」：如果要删除的节点有两个子节点，这就比较复杂了。我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点上。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点（如果有左子结点，那就不是最小节点了），所以，我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 88

前面两种情况稍微简单一些，第三种情况，我制作了一张动态图，希望能对你有所帮助。

动图封面

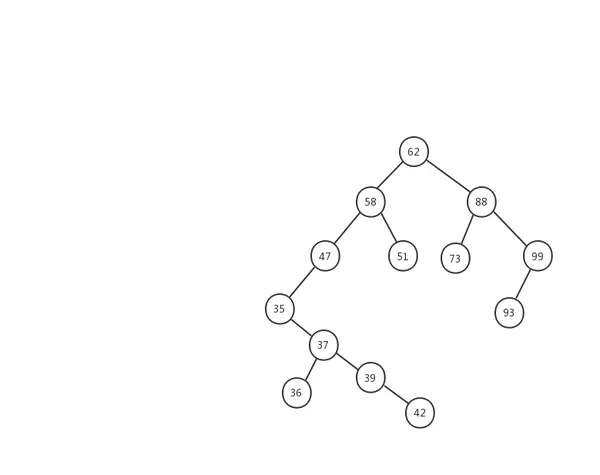
我们来看看二叉查找树的删除操作实现代码

void delete(TreeNode** tree, int data) {
    TreeNode* p = *tree; // p指向要删除的节点，初始化指向根节点
    TreeNode* pp = NULL; // pp记录的是p的父节点
    while (p != NULL && p->data != data) {
        pp = p;
        if (data > p->data) p = p->right;
        else p = p->left;
    }
    if (p == NULL) return; // 没有找到

    // 要删除的节点有两个子节点
    if (p->left != NULL && p->right != NULL) { // 查找右子树中最小节点
        TreeNode* minP = p->right;
        TreeNode* minPP = p; // minPP表示minP的父节点
        while (minP->left != NULL) {
            minPP = minP;
            minP = minP->left;
        }
        p->data = minP->data; // 将minP的数据替换到p中
        p = minP; // 下面就变成了删除minP了
        pp = minPP;
    }

    // 删除节点是叶子节点或者仅有一个子节点
    TreeNode* child; // p的子节点
    if (p->left != NULL) child = p->left;
    else if (p->right != NULL) child = p->right;
    else child = NULL;

    if (pp == NULL) *tree = child; // 删除的是根节点
    else if (pp->left == p) pp->left = child;
    else pp->right = child;

    free(p); // 释放被删除节点的内存
}

二叉查找树在极端情况下会退化成链表，例如每个节点都只有一个左节点，这是时间复杂度就变成了 O(n)，为了避免这种情况，又出现了一种新的树叫「平衡二叉查找树」

之后会开坑讲一下

≡