后悔数据结构当初没有好好学的第n天
现在恶补，知识学爆

基础操作：

• 查找元素：根据值查找节点位置
• 指定位置插入：在特定位置插入新节点
• 指定位置获取：获取特定位置的节点值
• 指定位置删除：删除特定位置的节点
• 获取长度：统计链表中节点的数量

	题目描述	主要实现思路
BM1	反转链表	使用三指针（prev、curr、next）迭代反转：保存下一个节点，反转当前指向，移动指针。返回prev作为新头。
BM2	链表内指定区间反转	引入虚拟头结点定位第m-1个节点（pre）。然后在[m,n]区间执行(n-m)次头插法（逐个将下一个节点插入pre后）。
BM3	链表中的节点每k个一组翻转	每k个节点为一组，使用反转链表方法局部反转。若剩余不足k个，则保持原序。递归或迭代均可，推荐迭代分段处理。
BM4	合并两个排序的链表	双指针模拟归并排序：比较两个链表当前节点值，小者接入新链表，移动对应指针。处理剩余部分。
BM5	合并k个已排序的链表	使用小根堆（优先队列）维护k个链表头结点，每次弹出最小值并接入结果链表，同时推入其下一个节点。
BM6	判断链表中是否有环	快慢指针（Floyd判圈算法）：fast每次走2步，slow走1步。若相遇则有环，否则无环。
BM7	链表中环的入口结点	先用快慢指针相遇于环内某点，再令一指针从头启动，与慢指针同步移动，相遇处即环入口。
BM8	链表中倒数最后k个结点	快慢指针：fast先走k步，然后slow与fast同步移动，至fast到尾时slow即为倒数第k个节点。
BM9	删除链表的倒数第n个节点	同BM8定位倒数第n+1个节点（pre），然后pre.next = pre.next.next删除目标节点。注意头节点特殊处理。
BM10	两个链表的第一个公共结点	双指针同步走：先计算长度差，长者先走差值步；或让指针走完一链表后换另一链表，总路程相等时相遇即公共节点。
BM11	链表相加(二)	模拟加法从低位到高位（需先反转链表或用栈），处理进位。结果可能需反转回原序。
BM12	单链表的排序	归并排序（自底向上）：分段合并有序子链表，或快慢指针找中点递归归并。时间O(n log n)。
BM13	判断一个链表是否为回文结构	快慢指针找中点，反转后半部分，与前半部分逐节点比较值是否相等。恢复链表可选。
BM14	链表的奇偶重排	分离奇偶位节点成两个链表（odd、even），然后even接odd尾部。注意偶数长度处理。
BM15	删除有序链表中重复的元素-I	单指针遍历：若当前节点与下一节点值相同，跳过下一节点（保留首次出现）。
BM16	删除有序链表中重复的元素-II	引入虚拟头结点，双指针或单指针遍历：若连续重复，跳过整个重复段（一个不留）。

---

一般会给出一个最基础的链表

function ListNode(val, next) {
    this.val = (val === undefined ? 0 : val);
    this.next = (next === undefined ? null : next);
}

• 节点包含两个成员：
  • val：存储节点的值，通常为整数（int），题目中 |val| ≤ 1000。
  • next：指向下一个节点的指针（引用），类型为同类 ListNode*（或 ListNode），初始可能为 NULL/null/None
• 无哑头节点（dummy head）：输入的 head 就是真实头结点（有有效值），除非题目特别说明
• 单向链表：只能从头到尾遍历，无前向指针
• 输入形式：
  • 函数签名通常为 ListNode* head（或类似），可能额外传入其他参数（如 m、n、k 等）
  • 空链表：head = NULL / null / None
• 输出形式：
  • 大多数题目要求返回新的头结点（ListNode*）
  • 操作通常要求原地修改，以满足空间复杂度 O(1)

---

常见操作

单链表常见操作的实现方法

以下针对单链表（节点结构为 val 和 next）的几种常见操作，提供标准、高效的实现思路。所有操作均基于从头结点开始遍历，时间复杂度与空间复杂度分析清晰。假设节点定义如下（以 JavaScript 为例，其他语言类似）：

function ListNode(val, next) {
    this.val = val;
    this.next = next || null;
}

1. 查找元素：根据值查找节点位置（返回位置或节点）

思路：从头遍历，逐个比较节点值，直到找到匹配值或到达链表末尾。

实现要点：

• 返回第一个匹配节点的位置（从 1 开始）或节点本身。
• 未找到返回 -1 或 null。

function findNode(head, target) {
    let pos = 1;
    let curr = head;
    while (curr !== null) {
        if (curr.val === target) {
            return pos;  // 或 return curr; 返回节点本身
        }
        curr = curr.next;
        pos++;
    }
    return -1;  // 未找到
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)

2. 指定位置插入：在第 i 个位置插入新节点（i 从 1 开始）

思路：遍历到第 i-1 个节点，将新节点插入其后。特殊处理插入到头部（i=1）。

实现要点：

• 若 i=1，新节点成为新头。
• 若 i > 长度，插入失败或插入尾部（视题目要求）。

function insertAtPosition(head, i, val) {
    let newNode = new ListNode(val);
    if (i === 1) {
        newNode.next = head;
        return newNode;  // 新头结点
    }
    
    let curr = head;
    for (let pos = 1; pos < i - 1 && curr !== null; pos++) {
        curr = curr.next;
    }
    if (curr === null) return head;  // i 超出范围，不插入
    
    newNode.next = curr.next;
    curr.next = newNode;
    return head;
}

• 时间复杂度：O(i) → 最坏 O(n)
• 空间复杂度：O(1)

3. 指定位置获取：获取第 i 个节点的値（i 从 1 开始）

思路：遍历 i-1 步，直接返回当前节点的值。

function getAtPosition(head, i) {
    let curr = head;
    for (let pos = 1; pos < i && curr !== null; pos++) {
        curr = curr.next;
    }
    return curr ? curr.val : null;  // 未找到返回 null
}

• 时间复杂度：O(i) → 最坏 O(n)
• 空间复杂度：O(1)

4. 指定位置删除：删除第 i 个节点（i 从 1 开始）

思路：遍历到第 i-1 个节点，修改其 next 指向跳过第 i 个节点。特殊处理删除头结点。

function deleteAtPosition(head, i) {
    if (head === null) return null;
    if (i === 1) return head.next;  // 删除头结点
    
    let curr = head;
    for (let pos = 1; pos < i - 1 && curr !== null; pos++) {
        curr = curr.next;
    }
    if (curr === null || curr.next === null) return head;  // i 超出范围
    
    curr.next = curr.next.next;  // 跳过第 i 个节点
    return head;
}

• 时间复杂度：O(i) → 最坏 O(n)
• 空间复杂度：O(1)

5. 获取链表长度（节点数量）

思路：遍历链表，累计计数。

function getLength(head) {
    let len = 0;
    let curr = head;
    while (curr !== null) {
        len++;
        curr = curr.next;
    }
    return len;
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)

---

反转链表

BM1 | 全量反转链表

给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围： 0≤n≤10000≤n≤1000

要求：空间复杂度 O(1)O(1) ，时间复杂度 O(n)O(n) 。

如当输入链表{1,2,3}时，

经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。

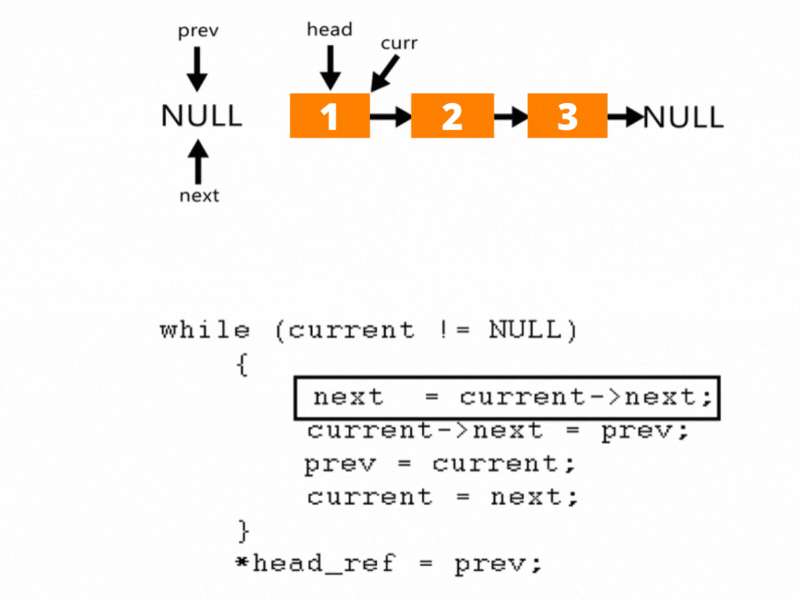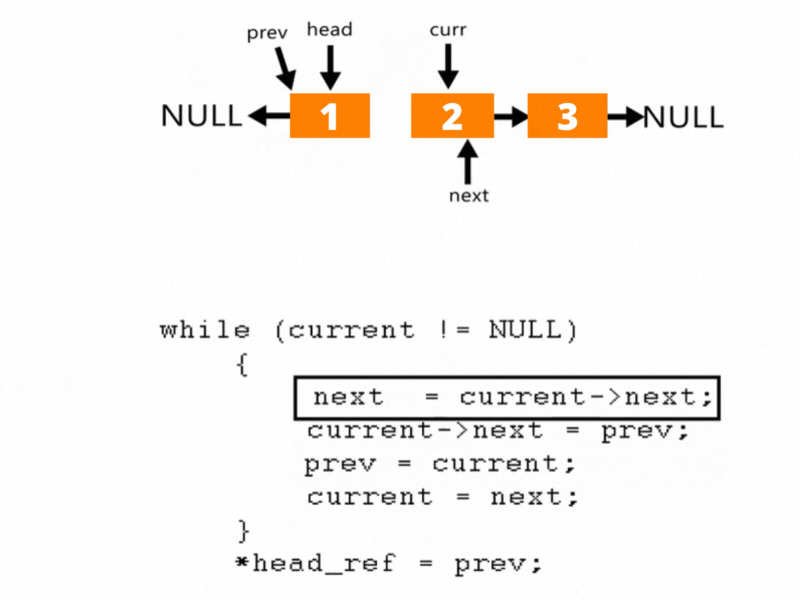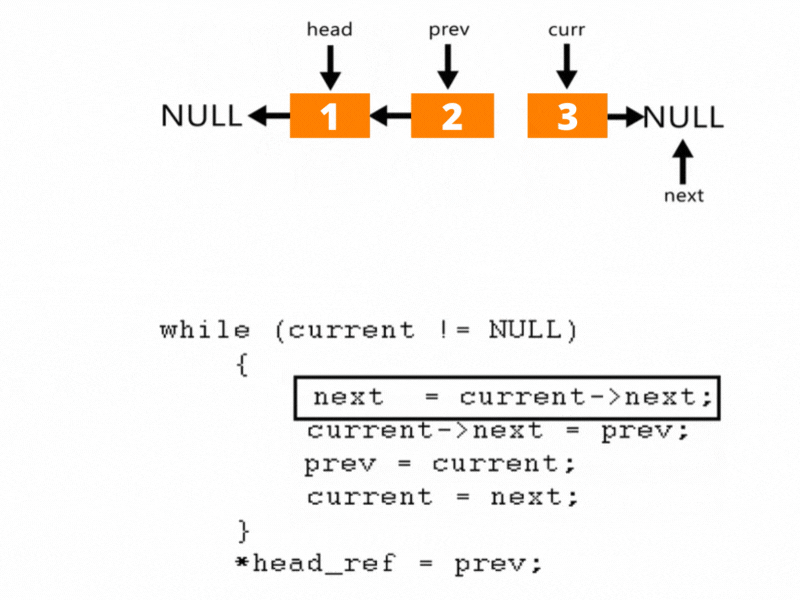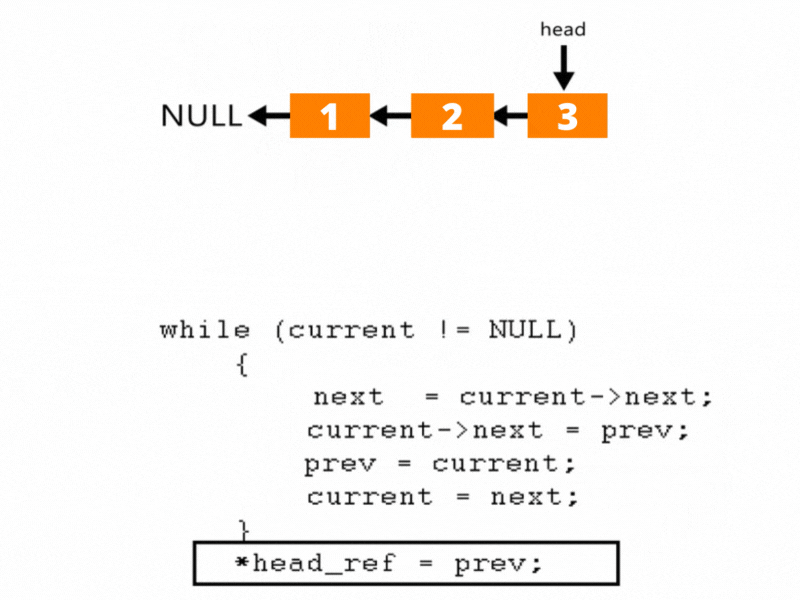
以上转换过程如下图所示：

---

解法：

• 初始化 prev 为 null（新链表的尾部）。
• current 从链表头节点开始。
• 在循环中：
  • 暂存 next = current.next（避免指针丢失）。
  • 将 current.next 指向 prev（反转当前指针）。
  • 更新 prev = current（前移 prev）。
  • 更新 current = next（前移 current）。
• 循环结束后，prev 指向原链表的尾节点（新头节点），更新 list.head = prev。

其实就是三指针原地反转

export function ReverseList(head: ListNode): ListNode {
    let prev = null;
    let curr = head;

    while (curr !== null) {
    
        // 保存下一个节点，防止断链
        let next = curr.next;

        // 反转当前节点的指向
        curr.next = prev;

        // 指针向前移动
        prev = curr;
        curr = next;
    }
    // prev 指向反转后的新头结点
    return prev;
};

BM2 | 反转链表部分区间

给定一个单链表的头结点 head，长度为 n，反转该链表从位置 m 到 n 的部分，返回反转后的链表。

数据范围： 0≤m≤n≤n≤1000 ，链表中任意节点的值满足 |val|≤1000

例如：
给出的链表为 1→2→3→4→5→NULL1→2→3→4→5→NULL, m=2,n=4m=2,n=4,
返回 1→4→3→2→5→NULL1→4→3→2→5→NULL.

要实现原地反转指定区间，需要：

1. 找到反转区间的前一个节点（pre），即第 m-1 个节点。
2. 找到反转区间的最后一个节点（记为 end），即第 n 个节点。
3. 将 [m, n] 区间使用经典链表反转方法进行原地反转。
4. 正确连接反转后的区间与前后部分：
   • pre.next 指向反转后区间的新的头节点（原第 n 个节点）。
   • 反转后区间的尾节点（原第 m 个节点）指向 end.next。

关键操作：

• 先遍历定位到 pre 和反转区间的起始节点 start（第 m 个节点）。
• 然后在 [start, end] 区间内使用三指针迭代反转。
• 最后调整指针连接。

export function reverseBetween(head: ListNode | null, m: number, n: number): ListNode | null {
    if (head === null || m === n) return head;

    const dummy = new ListNode(0);
    dummy.next = head;
    let pre = dummy;

    // 移动到第 m-1 个节点
    for (let i = 0; i < m - 1; i++) {
        pre = pre.next!;
    }

    let start = pre.next!;   // 第 m 个节点（反转区间的原头部）
    let then = start.next;   // 第 m+1 个节点（待头插的节点）

    // 执行 (n - m) 次头插
    for (let i = 0; i < n - m; i++) {
        start.next = then.next;   // 从原区间摘除 then
        then.next = pre.next;     // then 插入 pre 之后（成为新头部）
        pre.next = then;          // 更新 pre 的 next
        then = start.next;        // 更新 then 为下一个待移动节点
    }

    return dummy.next;
}

---