简单刷个力扣百题，完球了这玩意从大二下开坑以来就没刷完，现在后端转前端也要那前端那一套来过一趟，还有几天字节面试了都

---

1.两数之和

给定一个整数数组 nums 和一个整数目标值 target
在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标
你可以假设每种输入只会对应一个答案，并且同一个元素不能重复使用

示例：
输入：nums = [2,7,11,15], target = 9
输出：[0,1] 解释：因为 nums[0] + nums[1] = 2 + 7 = 9。

直接用双重循环解，优化的话其实可以上哈希表

function twoSum(nums: number[], target: number): number[] {
    for (let i = 0; i < nums.length; i++) {
        for (let j = i + 1; j < nums.length; j++) {
            if (nums[i] + nums[j] === target) {
                return [i, j];
            }
        }
    }
    return [];
}

---

2.两数相加

给定两个非空单向链表，表示两个非负整数
每个节点存储一位数字，数字以逆序存储（个位在头部），要求返回一个新链表表示它们的和（同样逆序存储）
不允许修改原链表

示例：
输入：l1 = 2 → 4 → 3（表示 342），l2 = 5 → 6 → 4（表示 465）
输出：7 → 0 → 8（表示 807）

本质上是模拟竖式加法，从低位到高位逐位相加。由于链表逆序存储，正好从个位开始遍历

1. 逐位相加并处理进位：
   • 同时遍历两个链表的节点，取当前节点值相加，加上上一位的进位（初始进位为 0）。
   • 当前位结果 = (val1 + val2 + carry) % 10
   • 新进位 carry = Math.floor((val1 + val2 + carry) / 10)
2. 使用哑节点（dummy head）简化代码：
   • 创建一个哑节点，尾指针指向它，便于统一处理头部节点，避免单独处理第一个节点。
3. 处理链表长度不等和最终进位：
   • 当一个链表遍历完时，将另一个链表的剩余节点视为 val = 0 继续相加。
   • 遍历结束后，若仍有进位（carry = 1），需添加一个新节点值为 1。

提供以下 ListNode 类型定义：

class ListNode {
  val: number;
  next: ListNode | null;
  constructor(val?: number, next?: ListNode | null) {
    this.val = val === undefined ? 0 : val;
    this.next = next === undefined ? null : next;
  }
}

题解

function addTwoNumbers(l1: ListNode | null, l2: ListNode | null): ListNode | null {
  const dummy: ListNode = new ListNode(0);
  // 哑节点，没有 dummy，直接从第一个节点开始构建，结果链表的头节点会在循环中不断变化
  //需要额外判断是否是第一个节点
  let tail: ListNode = dummy;
  //始终指向结果链表的“当前最后一个节点”。
  //每次计算出一位新数字后，直接在 tail 后面添加新节点
  let carry: number = 0;
  // 进位，当前这一位加完后，是否需要给下一位（更高位）额外加 1

  while (l1 !== null || l2 !== null || carry !== 0) {
    const val1: number = l1 ? l1.val : 0;
    const val2: number = l2 ? l2.val : 0;

    const sum: number = val1 + val2 + carry;
    const digit: number = sum % 10;
    carry = Math.floor(sum / 10);

    tail.next = new ListNode(digit);
    tail = tail.next;

    if (l1) l1 = l1.next;
    if (l2) l2 = l2.next;
  }

  return dummy.next;
}

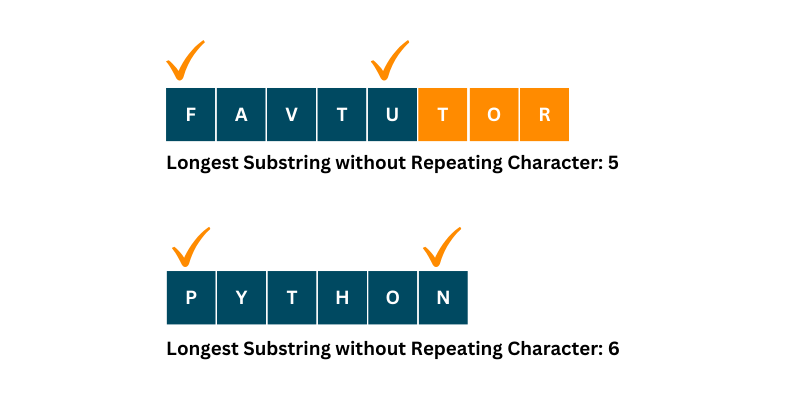
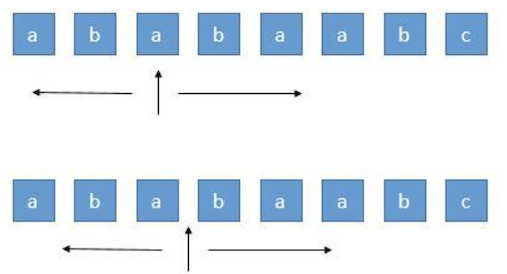
3.无重复字符的最长子串

要求给定一个字符串 s，找出其中不含有重复字符的最长子串的长度
（而非子序列）

示例：

• 输入：”abcabcbb” → 输出：3（子串 “abc”）
• 输入：”bbbbb” → 输出：1
• 输入：”pwwkew” → 输出：3（子串 “wke”）

直接上滑动窗口，结合哈希集合（Set）或映射

• 使用左指针 left 和右指针 right 维护一个窗口 (left, right)
• 扩展右指针，若遇到重复字符，则收缩左指针直到无重复
• 每次更新最大长度 maxLength = Math.max(maxLength, right - left)

function lengthOfLongestSubstring(s: string): number {
    const charSet = new Set<string>();  // 记录窗口内字符
    let left = 0;                       // 左指针
    let maxLength = 0;                  // 最大长度

    for (let right = 0; right < s.length; right++) {
        // 若当前字符已存在，收缩左指针
        while (charSet.has(s[right])) {
            charSet.delete(s[left]);
            left++;
        }
        charSet.add(s[right]);
        maxLength = Math.max(maxLength, right - left + 1);
    }

    return maxLength;
}

---

4.寻找两个正序数组的中位数

要求在两个已排序数组 nums1 和 nums2 中找到合并后的中位数，且时间复杂度必须为 O(log(m + n))，其中 m 和 n 分别为数组长度

示例：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

最初思路

最开始打算做双指针合并，使用两个指针 i 和 j 分别指向 nums1 和 nums2 的当前待比较位置（初始为 0），每次比较 nums1[i] 和 nums2[j]，将较小的元素放入结果数组 merged，并将对应指针后移，当某个数组遍历完后，将另一个数组剩余元素全部追加到 merged，合并完成后，merged 就是一个完整有序数组

然后就可以根据总长度奇偶性计算中位数：
奇数直接取第 (total+1)/2 个元素（索引 mid）
偶数取第 total/2 和第 total/2 + 1 个元素的平均（索引 mid-1 和 mid）

想了 40 分钟，但是复杂度 m * n，直接寄了

function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
    const merged: number[] = [];

    for (let i = 0; i < nums1.length; i++) {
        for (let j = 0; j < nums2.length; j++) {
        while(nums2[j] <= nums1[i]);
            merged.push(nums2[j]);
        }
        merged.push(nums1[i]);
    }

    for (let k = 0; k < nums2.length; k++) {
        merged.push(nums2[k]);
    }

    const total = merged.length;
    const mid = Math.floor(total / 2);
    return total % 2 === 1 ? merged[mid] : (merged[mid - 1] + merged[mid]) / 2;
}

改进

• 外层 for：遍历 nums1 的每一个元素 nums1[i]。
• 内层 while（代替 for，避免重复遍历）：在放入 nums1[i] 之前，先检查 nums2 的头部元素（nums2[0]）。
  • 只要 nums2[0] <= nums1[i]，就说明这个元素应该排在 nums1[i] 前面，先放入 merged，并从 nums2 中移除（使用 shift()）。
  • 这样保证了顺序正确。
• 放入当前 nums1[i]。
• 外层循环结束后，如果 nums2 还有剩余元素（说明它们都大于 nums1 所有元素），直接全部追加。

function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
  const merged: number[] = [];

  // 外层循环遍历 nums1 的每个元素
  for (let i = 0; i < nums1.length; i++) {
    // 在放入 nums1[i] 之前，先把 nums2 中所有小于等于 nums1[i] 的元素放入
    while (nums2.length > 0 && nums2[0] <= nums1[i]) {
      merged.push(nums2.shift()!); // 取出 nums2 头部元素
    }
    // 放入当前 nums1[i]
    merged.push(nums1[i]);
  }
  // 处理 nums2 中剩余的所有元素（如果 nums2 还有）
  while (nums2.length > 0) {
    merged.push(nums2.shift()!);
  }

  const total = merged.length;
  const mid = Math.floor(total / 2);

  if (total % 2 === 1) {
    return merged[mid];
  } else {
    return (merged[mid - 1] + merged[mid]) / 2;
  }
}

二分法

暴力合并为 O(m + n)，但题目要求对数复杂度，因此需避免完整合并。核心思路是将问题转化为在较短数组上二分查找一个分区点，使左右部分满足中位数条件：

• 总元素数 total = m + n。
• 中位数位置：若 total 奇数，为第 (total + 1)/2 个元素；若偶数，为第 total/2 和第 total/2 + 1 个元素的平均。
• 我们需要在合并数组的“左侧”选取 total/2 个元素（使用 (total + 1)/2 以统一奇偶处理）。
• 在较短数组 A 上二分查找左侧元素个数 i（0 ≤ i ≤ m），则较长数组 B 左侧元素个数 j = (total + 1)/2 - i。
• 分区条件：
  • 左侧最大值 ≤ 右侧最小值：max(A[i-1], B[j-1]) ≤ min(A[i], B[j])。
• 处理边界：使用 -∞ 和 +∞ 填充空侧。

算法步骤

1. 确保 nums1 为较短数组（若不是，交换）。
2. 二分范围：low = 0, high = nums1.length。
3. 计算分区：i = (low + high) / 2, j = (m + n + 1) / 2 - i。
4. 检查分区：
   • 若 A[i-1] > B[j]，则 i 太大，high = i - 1。
   • 若 B[j-1] > A[i]，则 i 太小，low = i + 1。
   • 否则，分区正确。
5. 计算中位数：
   • 左侧最大：max(A[i-1], B[j-1])。
   • 右侧最小：min(A[i], B[j])。
   • 若 total 奇数，返回左侧最大；偶数，返回平均。

function findMedianSortedArrays(nums1: number[], nums2: number[]): number {
    const merged: number[] = [];

    // 外层循环遍历 nums1 的每个元素
    for (let i = 0; i < nums1.length; i++) {
        // 在放入 nums1[i] 之前，先把 nums2 中所有小于等于 nums1[i] 的元素放入 merged
        while (nums2.length > 0 && nums2[0] <= nums1[i]) {
            merged.push(nums2.shift()!);  // 取出 nums2 头部元素
        }

        // 放入当前 nums1[i]
        merged.push(nums1[i]);
    }

    // 处理 nums2 中剩余的所有元素（如果 nums2 还有）
    while (nums2.length > 0) {
        merged.push(nums2.shift()!);
    }

    const total = merged.length;
    const mid = Math.floor(total / 2);

    if (total % 2 === 1) {
        return merged[mid];
    } else {
        return (merged[mid - 1] + merged[mid]) / 2;
    }
}

---

5.最长的回文子串

要求给定一个字符串 s，返回其中最长的回文子串（回文指正读反读相同的连续子串）
示例：

• 输入：”babad” → 输出：”bab” 或 “aba”（长度 3）
• 输入：”cbbd” → 输出：”bb”（长度 2）

中心扩展法（Expand Around Center）

时间复杂度 O(n²)，空间复杂度 O(1)

思路

回文串以中心对称。中心可能为单个字符（奇数长度回文）或两个相同字符间（偶数长度回文）。 对于字符串每个可能中心（共 2n-1 个），向两侧扩展比较字符，直至不对称。记录扩展中最长回文。

步骤：

1. 遍历字符串索引 i 从 0 到 n-1。
2. 以 i 为中心扩展奇数长度回文。
3. 以 i 和 i+1 为中心扩展偶数长度回文。
4. 每次扩展更新最长回文起点和长度。
5. 返回对应子串。

TypeScript 实现

function longestPalindrome(s: string): string {
    if (s.length < 2) return s;

    let start = 0;      // 最长回文起点
    let maxLength = 1;  // 最长回文长度（初始至少 1）

    function expandAroundCenter(left: number, right: number) {
        while (left >= 0 && right < s.length && s[left] === s[right]) {
            const currentLength = right - left + 1;
            if (currentLength > maxLength) {
                start = left;
                maxLength = currentLength;
            }
            left--;
            right++;
        }
    }

    for (let i = 0; i < s.length; i++) {
        // 奇数长度回文（中心为 i）
        expandAroundCenter(i, i);
        // 偶数长度回文（中心为 i 和 i+1）
        expandAroundCenter(i, i + 1);
    }

    return s.substring(start, start + maxLength);
}

---

6. Z 字变换

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P A H N
A P L S I I G
Y I R

之后输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"

实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

示例 1：

输入：s = “PAYPALISHIRING”, numRows = 3
输出：”PAHNAPLSIIGYIR”

示例 2：

输入：s = “PAYPALISHIRING”, numRows = 4
输出：”PINALSIGYAHRPI”
解释：
P I N
A L S I G
Y A H R
P I

TypeScript 实现

直接计算位置

function convert(s: string, numRows: number): string {
  if (numRows === 1) return s;

  let result = "";
  const cycle = 2 * numRows - 2;

  for (let row = 0; row < numRows; row++) {
    for (let i = 0; i + row < s.length; i += cycle) {
      result += s[i + row];
      if (row !== 0 && row !== numRows - 1 && i + cycle - row < s.length) {
        result += s[i + cycle - row];
      }
    }
  }

  return result;
}

---

7. 整数反转

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0
假设环境不允许存储 64 位整数（有符号或无符号

示例 1：
输入：x = 123
输出：321

示例 2：
输入：x = -123
输出：-321

没啥好讲的，转字符串反转再转回去，处理一下负号和边界情况就成

反转字符串

const reverseString = (str: string): string => str.split("").reverse().join("");

function reverse(x: number): number {
  if (x === 0) {
    return x;
  }
  const MAX = 2 ** 31 - 1;
  const MIN = -(2 ** 31);

  let mid = x.toString();
  let LI: boolean = true;
  if (mid[0] === "-") {
    LI = false;
  }
  const reverseString = mid.split("").reverse().join("");
  if (LI === true) {
    if (parseInt(reverseString) < MIN || parseInt(reverseString) > MAX) {
      return 0;
    }
    return parseInt(reverseString);
  }
  if (LI === false) {
    let fin = reverseString.slice(0, reverseString.length - 1);
    let fin2 = -parseInt(fin);
    if (fin2 < MIN || fin2 > MAX) {
      return 0;
    }
    return fin2;
  }
}

---

8.字符串转换整数

实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数。

函数 myAtoi(string s) 的算法如下：

1. 空格：读入字符串并丢弃无用的前导空格（" "）
2. 符号：检查下一个字符（假设还未到字符末尾）为 '-' 还是 '+'如果两者都不存在，则假定结果为正
3. 转换：通过跳过前置零来读取该整数，直到遇到非数字字符或到达字符串的结尾，如果没有读取数字，则结果为 0
4. 舍入：如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被舍入为 −231 ，大于 231 − 1 的整数应该被舍入为 231 − 1

function myAtoi(s: string): number {
  let max = 2 ** 31 - 1;
  let min = -(2 ** 31);

  let i: number = 0;
  let sign: number = 1;
  let fin = "";
  let clac = 0;

  if (i <= s.length) {
    while (s[i] === " ") {
      i++;
    }

    while (s[i] === "-" || s[i] === "+") {
      if (s[i] === "-") {
        sign = -1;
      }
      if (s[i] === "+") {
        sign = 1;
      }
      if (clac === 1) {
        return 0;
      }
      clac = 1;
      i++;
    }
    while (s[i] <= "9" && s[i] >= "0") {
      fin = fin + s[i];
      i++;
    }
    if (fin === "") return 0;
    if (sign === 1) {
      if (parseInt(fin) >= max) {
        return max;
      }
      if (parseInt(fin) <= min) {
        return min;
      }
      return parseInt(fin);
    }
    if (sign === -1) {
      if (-parseInt(fin) >= max) {
        return max;
      }
      if (-parseInt(fin) <= min) {
        return min;
      }
      return -fin;
    }
  }
}

没啥好说的，处理一下转换和条件判断的事情

---

9.回文数

给一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数
例如，121 是回文，而 123 不是

智斗程度堪比两数之和，转字符串逆序比较秒了

function isPalindrome(x: number): boolean {
  let arr = x.toString();
  let brr = arr.split("").reverse().join("");
  if (arr === brr) {
    return true;
  }
  if (arr !== brr) {
    return false;
  }
}

---

10.正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

• '.' 匹配任意单个字符
• '*' 匹配零个或多个前面的那一个元素

匹配是要涵盖 整个 字符串 s 的，而不是部分字符串。

示例 1：

输入：s = “aa”, p = “a”
输出：false
解释：”a” 无法匹配 “aa” 整个字符串。

示例 2:

输入：s = “aa”, p = “a“
输出：true
解释：因为 ‘‘ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。

示例 3：

输入：s = “ab”, p = “.“
输出：true
解释：”.“ 表示可匹配零个或多个（’*‘）任意字符（’.’）

这道题最开始是想要用纯同步双指针来解，没解出来

function isMatch(s: string, p: string): boolean {
  if (s == p) {
    return true;
  }
  let sindex = 0;
  let pindex = 0;

  while (sindex < s.length && pindex < p.length) {
    if (s[sindex] === p[pindex] || p[pindex] === ".") {
      sindex++;
      pindex++;
    }
    if (p[pindex] === "*") {
      while (s[sindex] === s[sindex + 1]) {
        sindex++;
      }
      pindex++;
    }
    if (s[sindex] !== p[pindex]) {
      if (p[pindex] !== "*" && p[pindex] !== ".") {
        return false;
      }
    }
    return true;
  }
}

↑ 错误答案

主要是该问题具有非确定性：同一个 “x*“ 可以有多种匹配方式（0 次、1 次、多次），需要尝试不同分支。纯同步双指针（单路径贪婪）无法处理回溯需求，会在某些案例中错误消耗字符，导致后续失败。

比如说在 s = “aaa”, p = “aba” 里贪婪匹配可能错误使用 “b“，而实际应跳过 “b*“（匹配 0 次）

因此不能用简单 while 循环同步双指针线性解决，必须引入分支或状态记录

然后题解就是使用 dp 解决：

定义二维布尔数组 dp[i][j] 表示：s 的前 i 个字符（s[0..i-1]）是否能被 p 的前 j 个字符（p[0..j-1]）匹配，最终答案为 dp[m][n]，其中 m = s.length，n = p.length

function isMatch(s: string, p: string): boolean {
  const m = s.length,
    n = p.length;
  const dp = Array(m + 1)
    .fill(null)
    .map(() => Array(n + 1).fill(false));

  dp[0][0] = true;
  for (let j = 2; j <= n; j++) {
    if (p[j - 1] === "*") {
      dp[0][j] = dp[0][j - 2];
    }
  }

  for (let i = 1; i <= m; i++) {
    for (let j = 1; j <= n; j++) {
      if (p[j - 1] === "*") {
        dp[i][j] =
          dp[i][j - 2] ||
          ((s[i - 1] === p[j - 2] || p[j - 2] === ".") && dp[i - 1][j]);
      } else {
        dp[i][j] =
          (s[i - 1] === p[j - 1] || p[j - 1] === ".") && dp[i - 1][j - 1];
      }
    }
  }

  return dp[m][n];
}

初始化:

空串与空模式dp[0][0] = true：空字符串可以被空模式匹配。
空字符串与非空模式 只有当模式中某些 “x*” 可以匹配 0 次字符时，才可能匹配空字符串。 因此从左向右扫描模式：

for (let j = 2; j <= n; j++) {
    if (p[j-1] === '*') {
        dp[0][j] = dp[0][j-2];  // 直接继承“跳过当前 x*”的状态
    }
}

示例：p = “abc*“ 可以匹配空字符串，故 dp[0][2]、dp[0][4]、dp[0][6] 均为 true。

状态转移方程

遍历 i = 1..m 和 j = 1..n，根据 p[j-1] 的类型分为两种情况：

1. 当前模式字符不是 ‘*‘（普通字符或 ‘.’） 只能进行单字符匹配：

   dp[i][j] = (s[i-1] === p[j-1] || p[j-1] === '.') && dp[i-1][j-1];

   含义：当前字符匹配且前一个子问题也匹配，则当前子问题成立。

2. 当前模式字符是 ‘*‘（与前一个字符组成 “x”） ‘‘ 提供了两种选择：

   • 匹配 0 次：直接跳过整个 “x*”，状态等同于 dp[i][j-2]。
   • 匹配 1 次或多次：前提是当前 s[i-1] 能与 “x” 匹配（s[i-1] === p[j-2] 或 p[j-2] === '.'），且在上一个字符已匹配的基础上继续使用 “x*” 匹配当前字符，即 dp[i-1][j]

   两者任一成立即可：

   dp[i][j] = dp[i][j-2] ||
             ((s[i-1] === p[j-2] || p[j-2] === '.') && dp[i-1][j]);

时间与空间复杂度

• 时间复杂度：O(mn)，每个状态只计算一次。
• 空间复杂度：O(mn)，可进一步优化为 O(n)（仅使用两行或一行滚动数组）。