动态规划介绍

动态规划（Dynamic Programming，简称 DP）是一种算法设计范式，用于解决具有重叠子问题和最优子结构性质的优化问题。它通过将原问题分解为若干子问题，先解决子问题并保存结果（通常使用表格或数组），从而避免重复计算，最终构建出原问题的解。

动态规划的核心思想源于数学中的贝尔曼最优性原理：最优策略的子策略总是最优的。与分治法不同，动态规划适用于子问题重叠的情况，能将指数级时间复杂度优化至多项式级。

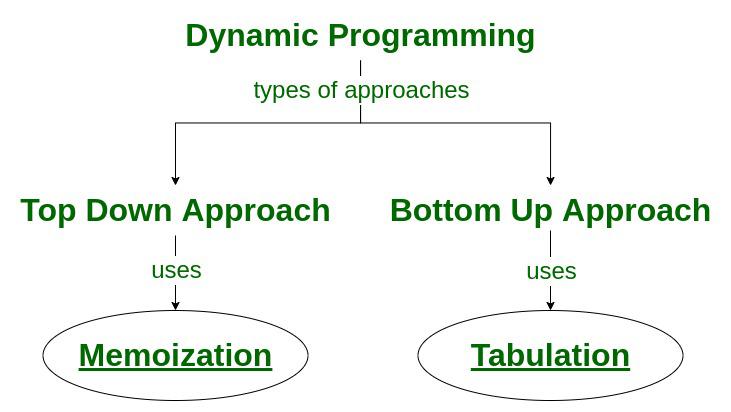
动态规划的适用条件

• 最优子结构：原问题的最优解可由子问题的最优解组合得出。
• 重叠子问题：子问题在递归求解中会被多次计算。

实现方式

• 自底向上（表格填充）：使用循环从小型子问题开始填充 DP 表格，直至原问题（常见于背包问题）。
• 自顶向下（记忆化递归）：递归求解并使用备忘录存储已计算子问题结果。

以 0/1 背包问题为例

0/1 背包问题（0/1 Knapsack Problem）是动态规划的经典应用：给定 n 个物品，每个物品有重量 w_i 和价值 v_i，以及一个容量为 W 的背包。每个物品只能选择取或不取（0/1），求背包中物品的最大总价值。

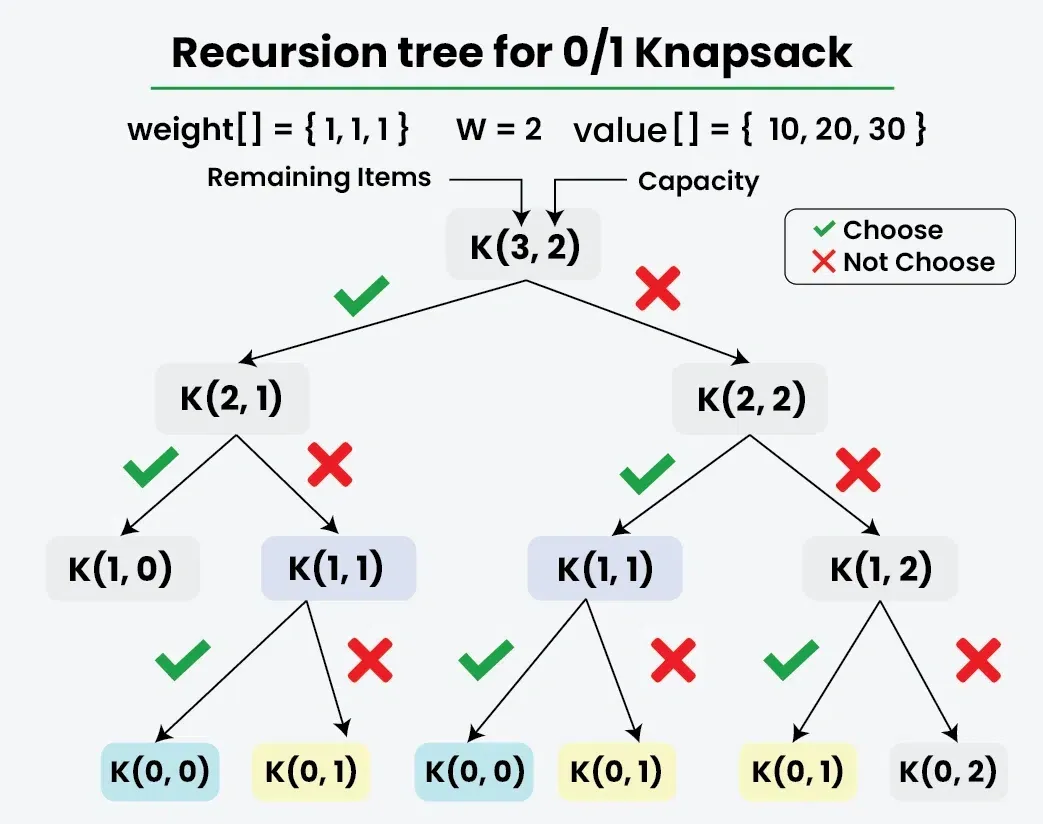
问题分析

• 子问题：考虑前 i 个物品和容量为 j 的背包的最大价值。
• 状态定义：dp[i][j] 表示前 i 个物品在容量 j 下的最大价值。
• 状态转移方程：
  • 不取第 i 个物品：dp[i][j] = dp[i-1][j]
  • 取第 i 个物品（若 j ≥ w_i）：dp[i][j] = dp[i-1][j - w_i] + v_i
  • dp[i][j] = max(以上两种情况)
• 边界：dp[0][j] = 0（无物品），dp[i][0] = 0（容量为 0）

示例

假设物品：重量[1, 3, 4]，价值[15, 20, 30]，背包容量 W = 4。
DP 表格填充过程如下所示：

初始状态（i=0，无物品）

容量 w:   0    1    2    3    4
物品 i
0        [0]  [0]  [0]  [0]  [0]

考虑第 1 个物品（重量 1，价值 15）

• 对于 w < 1：无法放入，只能取上一行值（0）。
• 对于 w ≥ 1：max(不放入: 0, 放入: 0 + 15) = 15。

容量 w:   0    1    2    3    4
物品 i
0        [0]  [0]  [0]  [0]  [0]
1        [0] [15] [15] [15] [15]

考虑第 2 个物品（重量 3，价值 20）

• 对于每个 w：
  • 如果 w < 3：无法放入，取上一行值。
  • 如果 w ≥ 3：max(不放入: dp[1][w], 放入: dp[1][w-3] + 20)。

计算示例：

• w=3：max(15, 15 + 20) = 35
• w=4：max(15, 15 + 20) = 35

容量 w:   0    1    2    3    4
物品 i
0        [0]  [0]  [0]  [0]  [0]
1        [0] [15] [15] [15] [15]
2        [0] [15] [15] [35] [35]

考虑第 3 个物品（重量 4，价值 30）

• 对于每个 w：
  • 如果 w < 4：无法放入，取上一行值。
  • 如果 w ≥ 4：max(不放入: dp[2][w], 放入: dp[2][w-4] + 30)。

计算示例：

• w=4：max(35, 0 + 30) = 35（不放入更好）

容量 w:   0    1    2    3    4
物品 i
0        [0]  [0]  [0]  [0]  [0]
1        [0] [15] [15] [15] [15]
2        [0] [15] [15] [35] [35]
3        [0] [15] [15] [35] [35]

最终结果：dp[3][4] = 35（选择第 1 和第 2 个物品：重量 1+3=4，价值 15+20=35）。

一维 DP 优化过程简要文本模拟

一维数组从后向前更新（避免覆盖）：

初始 dp: [0, 0, 0, 0, 0]（容量 0 到 4）

第 1 个物品后： [0, 15, 15, 15, 15]

第 2 个物品后： [0, 15, 15, 35, 35]

第 3 个物品后： [0, 15, 15, 35, 35]

复杂度分析

• 时间复杂度：O(n × capacity)
• 空间复杂度：二维 O(n × capacity)，一维 O(capacity)

伪代码（自底向上）

dp = 二维数组 (n+1) x (W+1)，初始化为 0

for i = 1 to n:
    for j = 1 to W:
        if w[i-1] > j:
            dp[i][j] = dp[i-1][j]
        else:
            dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i-1]] + v[i-1])

返回 dp[n][W]

时间复杂度 O(nW)，空间复杂度 O(nW)（可优化至 O(W) 使用一维数组）

动态规划通过系统地记录子问题解，避免了暴力递归的冗余计算，在组合优化、序列问题等领域广泛应用。理解背包问题有助于掌握 DP 的状态设计与转移核心。

0/1 背包问题的 TypeScript 实现详解

0/1 背包问题（0/1 Knapsack Problem）是动态规划的经典示例。给定 n 个物品，每个物品具有重量 weights[i] 和价值 values[i]，以及一个背包容量 capacity。每个物品只能选择放入或不放入（不可重复），目标是求背包内物品的最大总价值。

动态规划状态定义与转移

• 状态：dp[i][w] 表示考虑前 i 个物品（索引 0 到 i-1），背包容量为 w 时的最大价值。
• 转移方程：
  • 如果不放入第 i 个物品：dp[i][w] = dp[i-1][w]
  • 如果放入第 i 个物品（前提 w ≥ weights[i-1]）：dp[i][w] = dp[i-1][w - weights[i-1]] + values[i-1]
  • dp[i][w] = Math.max(不放入, 放入)
• 初始条件：dp[0][w] = 0（无物品），dp[i][0] = 0（容量为 0）。
• 结果：dp[n][capacity]

TypeScript 实现

以下提供两种实现：标准二维 DP 和空间优化的一维 DP（推荐，后者空间复杂度 O(capacity)）

1. 二维 DP 实现

function knapsack01(weights: number[], values: number[], capacity: number): number {
    const n = weights.length;
    // 创建 (n+1) x (capacity+1) 的二维数组，初始化为 0
    const dp: number[][] = Array.from({ length: n + 1 }, () => Array(capacity + 1).fill(0));

    for (let i = 1; i <= n; i++) {
        for (let w = 1; w <= capacity; w++) {
            if (weights[i - 1] > w) {
                // 重量超出，无法放入
                dp[i][w] = dp[i - 1][w];
            } else {
                // 取最大值
                dp[i][w] = Math.max(
                    dp[i - 1][w],                              // 不放入
                    dp[i - 1][w - weights[i - 1]] + values[i - 1]  // 放入
                );
            }
        }
    }

    return dp[n][capacity];
}

2. 一维 DP 实现（空间优化，使用滚动数组）

function knapsack01Optimized(weights: number[], values: number[], capacity: number): number {
    const n = weights.length;
    // 一维数组，dp[w] 表示容量 w 时的最大价值
    const dp: number[] = Array(capacity + 1).fill(0);

    for (let i = 0; i < n; i++) {
        // 从后向前遍历（防止覆盖前状态）
        for (let w = capacity; w >= weights[i]; w--) {
            dp[w] = Math.max(dp[w], dp[w - weights[i]] + values[i]);
        }
    }

    return dp[capacity];
}

示例

const weights = [1, 3, 4];
const values = [15, 20, 30];
const capacity = 4;

console.log(knapsack01Optimized(weights, values, capacity));  // 输出 35（放入重量 1 和 3 的物品）

• 物品数量 n = 3
• 重量 weights = [1, 3, 4]
• 价值 values = [15, 20, 30]
• 背包容量 capacity = 4